Cabtaxi Number

The 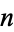th cabtaxi number is the smallest positive number that can be written in  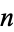ways as a sum of two (not necessarily positive) cubes. The name derived from the taxicab number, which is the smallest number representable in  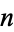ways as a sum of positive cubes. The first few are 1, 91, 728, 2741256, 6017193, 1412774811, 11302198488, 137513849003496, 424910390480793000, 933528127886302221000, ... (OEIS A047696), as listed below.

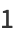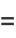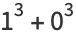			(1)
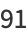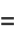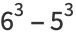			(2)
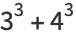			(3)
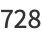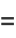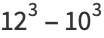			(4)
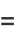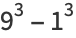			(5)
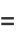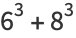			(6)
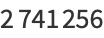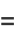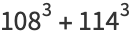			(7)
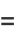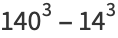			(8)
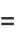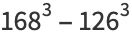			(9)
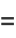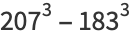			(10)
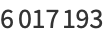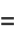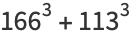			(11)
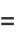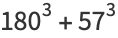			(12)
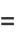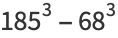			(13)
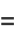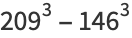			(14)
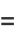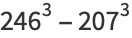			(15)
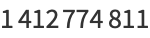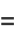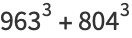			(16)
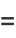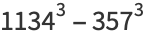			(17)
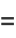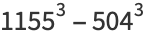			(18)
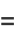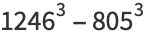			(19)
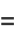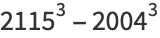			(20)
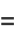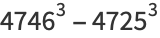			(21)
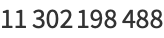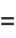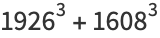			(22)
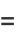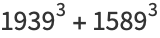			(23)
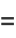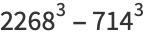			(24)
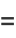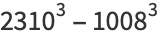			(25)
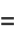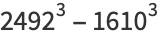			(26)
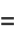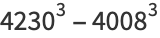			(27)
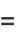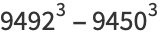			(28)
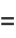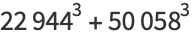			(29)
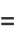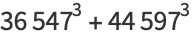			(30)
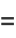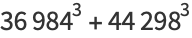			(31)
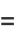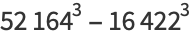			(32)
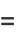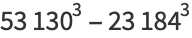			(33)
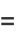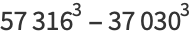			(34)
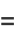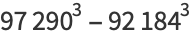			(35)
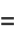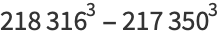			(36)
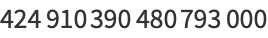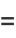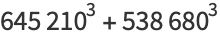			(37)
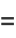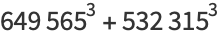			(38)
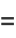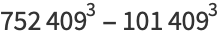			(39)
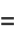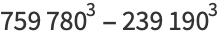			(40)
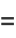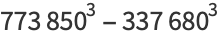			(41)
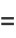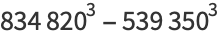			(42)
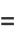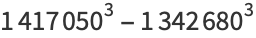			(43)
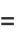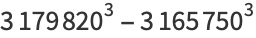			(44)
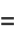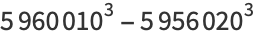			(45)
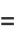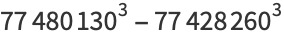			(46)
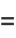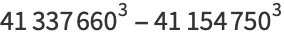			(47)
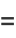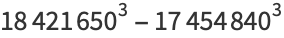			(48)
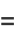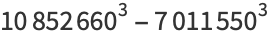			(49)
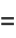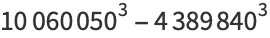			(50)
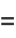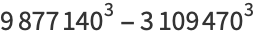			(51)
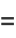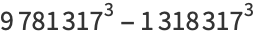			(52)
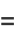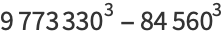			(53)
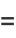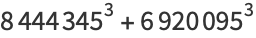			(54)
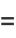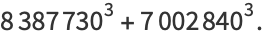			(55)

The 9th term was found by D. Moore (2005) and the 10th by Christian Boyer in 2006, the latter of which was independently verified by Hollerbach (2008).

REFERENCES:

Hollerbach, U. "Cabtaxi(10)." 16 May 2008. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0805&L=nmbrthry&T=0&P=1284.

Moore, D. "Cabtaxi(9)." 5 Feb 2005. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0502&L=nmbrthry&O=A&P=55.

Sloane, N. J. A. Sequence A047696 in "The On-Line Encyclopedia of Integer Sequences."