


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-7-2020
Date: 19-9-2020
Date: 2-2-2021
|
There are two definitions of the Carmichael function. One is the reduced totient function (also called the least universal exponent function), defined as the smallest integer 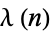 such that
such that 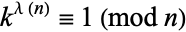 for all
for all  relatively prime to
relatively prime to  . The multiplicative order of
. The multiplicative order of 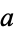 (mod
(mod 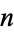 ) is at most
) is at most 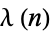 (Ribenboim 1989). The first few values of this function, implemented as CarmichaelLambda[n], are 1, 1, 2, 2, 4, 2, 6, 2, 6, 4, 10, ... (OEIS A002322).
(Ribenboim 1989). The first few values of this function, implemented as CarmichaelLambda[n], are 1, 1, 2, 2, 4, 2, 6, 2, 6, 4, 10, ... (OEIS A002322).
It is given by the formula
![lambda(n)=LCM[(p_i-1)p_i^(alpha_i-1)]_i,](https://mathworld.wolfram.com/images/equations/CarmichaelFunction/NumberedEquation1.gif) |
(1) |
where 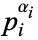 are primaries.
are primaries.
It can be defined recursively as
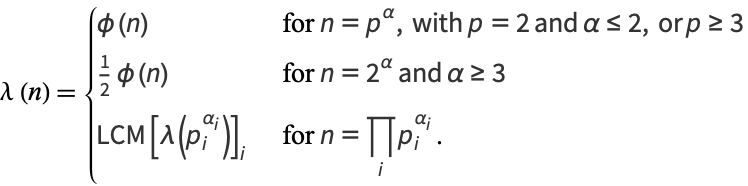 |
(2) |
Some special values include
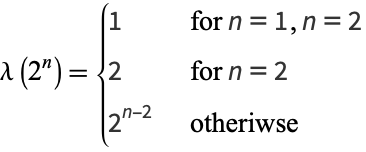 |
(3) |
and
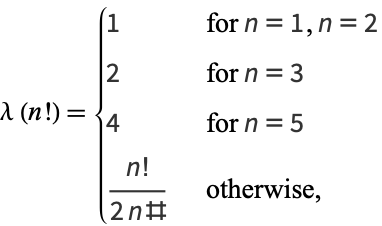 |
(4) |
where 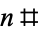 is a primorial (S. M. Ruiz, pers. comm., Jul. 5, 2009).
is a primorial (S. M. Ruiz, pers. comm., Jul. 5, 2009).
The second Carmichael's function 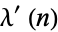 is given by the least common multiple (LCM) of all the factors of the totient function
is given by the least common multiple (LCM) of all the factors of the totient function 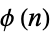 , except that if
, except that if 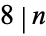 , then
, then 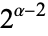 is a factor instead of
is a factor instead of 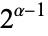 . The values of
. The values of 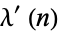 for the first few
for the first few 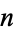 are 1, 1, 2, 2, 4, 2, 6, 4, 6, 4, 10, 2, 12, ... (OEIS A011773).
are 1, 1, 2, 2, 4, 2, 6, 4, 6, 4, 10, 2, 12, ... (OEIS A011773).
This function has the special value
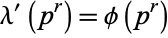 |
(5) |
for 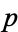 an odd prime and
an odd prime and 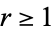 .
.
REFERENCES:
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, p. 27, 1989.
Riesel, H. "Carmichael's Function." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 273-275, 1994.
Sloane, N. J. A. Sequences A002322/M0298 and A011773 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, p. 226, 1991.



|
|
|
|
اختبار دم بسيط قد يكشف عن 12 نوعا من السرطان
|
|
|
|
|
|
|
الصين تكشف خططها لبناء محطة نووية على القمر
|
|
|
|
|
|
|
بالفيديو والصور: تزامنا مع ذكرى استشهاد الإمام الصادق (ع).. راية الحزن ترفرف قرب مرقد الإمام الحسين (ع)
|
|
|