


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2020
Date: 28-1-2021
Date: 14-9-2020
|
The Kronecker symbol is an extension of the Jacobi symbol 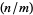 to all integers. It is variously written as
to all integers. It is variously written as 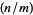 or
or 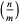 (Cohn 1980; Weiss 1998, p. 236) or
(Cohn 1980; Weiss 1998, p. 236) or 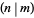 (Dickson 2005). The Kronecker symbol can be computed using the normal rules for the Jacobi symbol
(Dickson 2005). The Kronecker symbol can be computed using the normal rules for the Jacobi symbol
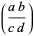 |
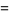 |
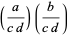 |
(1) |
 |
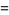 |
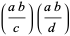 |
(2) |
 |
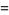 |
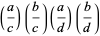 |
(3) |
plus additional rules for 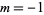 ,
,
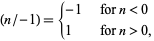 |
(4) |
and 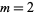 . The definition for
. The definition for 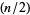 is variously written as
is variously written as
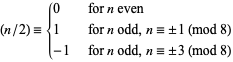 |
(5) |
or
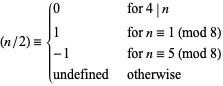 |
(6) |
(Cohn 1980). Cohn's form "undefines" 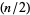 for singly even numbers
for singly even numbers 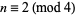 and
and 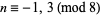 , probably because no other values are needed in applications of the symbol involving the binary quadratic form discriminants
, probably because no other values are needed in applications of the symbol involving the binary quadratic form discriminants 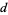 of quadratic fields, where
of quadratic fields, where 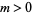 and
and 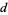 always satisfies
always satisfies 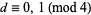 .
.
The Kronecker symbol is implemented in the Wolfram Language as KroneckerSymbol[n, m].
The Kronecker symbol 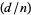 is a real number theoretic character modulo
is a real number theoretic character modulo 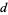 , and is, in fact, essentially the only type of real primitive character (Ayoub 1963).
, and is, in fact, essentially the only type of real primitive character (Ayoub 1963).
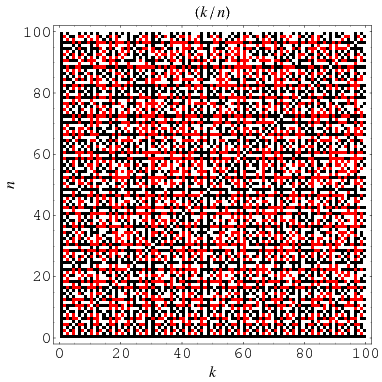
The illustration above and table below summarize 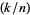 for
for 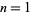 , 2, ... and small
, 2, ... and small 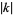 .
.
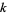 |
OEIS | period | 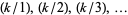 |
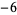 |
A109017 | 24 | 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 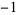 , 0, 0, 0, , 0, 0, 0, 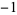 , 0, , 0, 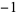 , 0, ... , 0, ... |
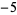 |
0 | 1, 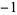 , 1, 1, 0, , 1, 1, 0, 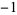 , 1, , 1, 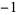 , 1, 0, , 1, 0, 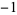 , 1, , 1, 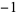 , , 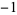 , 0, 1, , 0, 1, 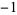 , , 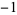 , , 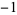 , 0, ... , 0, ... |
|
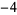 |
4 | 1, 0, 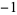 , 0, 1, 0, , 0, 1, 0, 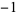 , 0, 1, 0, , 0, 1, 0, 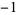 , 0, 1, 0, , 0, 1, 0, 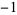 , 0, 1, 0, , 0, 1, 0, 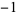 , 0, ... , 0, ... |
|
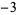 |
3 | 1, 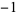 , 0, 1, , 0, 1, 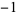 , 0, 1, , 0, 1, 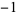 , 0, 1, , 0, 1, 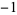 , 0, 1, , 0, 1, 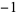 , 0, 1, , 0, 1, 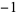 , 0, 1, , 0, 1, 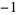 , ... , ... |
|
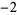 |
8 | 1, 0, 1, 0, 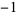 , 0, , 0, 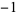 , 0, 1, 0, 1, 0, , 0, 1, 0, 1, 0, 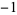 , 0, , 0, 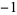 , 0, 1, 0, 1, 0, ... , 0, 1, 0, 1, 0, ... |
|
 |
A034947 | 1, 1, 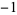 , 1, 1, , 1, 1, 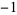 , , 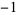 , 1, 1, 1, , 1, 1, 1, 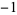 , , 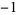 , 1, , 1, 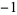 , , 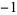 , 1, 1, ... , 1, 1, ... |
|
| 0 | 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ... | ||
| 1 | 1 | 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, ... | |
| 2 | A091337 | 8 | 1, 0, 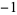 , 0, , 0, 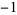 , 0, 1, 0, 1, 0, , 0, 1, 0, 1, 0, 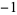 , 0, , 0, 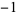 , 0, 1, ... , 0, 1, ... |
| 3 | A091338 | 1, 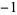 , 0, 1, , 0, 1, 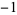 , 0, , 0, 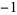 , , 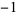 , 0, 1, 1, 0, 1, 1, 0, ... , 0, 1, 1, 0, 1, 1, 0, ... |
|
| 4 | A000035 | 2 | 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, ... |
| 5 | A080891 | 5 | 1, 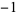 , , 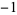 , 1, 0, 1, , 1, 0, 1, 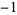 , , 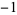 , 1, 0, 1, , 1, 0, 1, 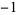 , , 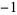 , 1, 0, ... , 1, 0, ... |
| 6 | 24 | 1, 0, 0, 0, 1, 0, 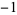 , 0, 0, 0, , 0, 0, 0, 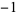 , 0, , 0, 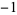 , 0, 0, 0, , 0, 0, 0, 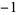 , 0, 1, 0, ... , 0, 1, 0, ... |
For values of 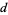 corresponding to primitive Dirichlet
corresponding to primitive Dirichlet 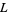 -series
-series 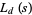 , the period of
, the period of 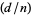 equals
equals 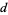 . For
. For 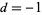 ,
, 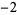 , ..., the periods of
, ..., the periods of 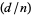 are 0, 8, 3, 4, 0, 24, 7, 8, 0, 40, 11, 6, ... (OEIS A117888) and for
are 0, 8, 3, 4, 0, 24, 7, 8, 0, 40, 11, 6, ... (OEIS A117888) and for 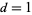 , 2, ... they are 1, 8, 0, 2, 5, 24, 0, 8, 3, 40, 0, 12, ... (OEIS A117889). Here, 0 indicates that the sequence is not periodic.
, 2, ... they are 1, 8, 0, 2, 5, 24, 0, 8, 3, 40, 0, 12, ... (OEIS A117889). Here, 0 indicates that the sequence is not periodic.
REFERENCES:
Ayoub, R. G. An Introduction to the Analytic Theory of Numbers. Providence, RI: Amer. Math. Soc., 1963.
Cohn, H. Advanced Number Theory. New York: Dover, p. 35, 1980.
Dickson, L. E. "Kronecker's Symbol." §48 in Introduction to the Theory of Numbers. New York: Dover, p. 77, 1957.
Sloane, N. J. A. Sequences A000035/M0001, A034947, A080891, A091337, A091338, A109017, A117888, and A117889 in "The On-Line Encyclopedia of Integer Sequences."
Weiss, E. Algebraic Number Theory. New York: Dover, 1998.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|