


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-5-2020
Date: 10-9-2020
Date: 20-10-2020
|
A Lambert series is a series of the form
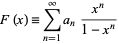 |
(1) |
for 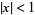 . Then
. Then
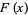 |
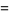 |
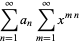 |
(2) |
 |
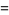 |
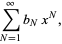 |
(3) |
where
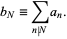 |
(4) |
The particular case 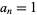 is sometimes denoted
is sometimes denoted
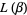 |
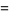 |
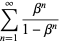 |
(5) |
 |
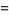 |
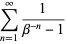 |
(6) |
 |
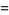 |
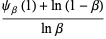 |
(7) |
for 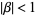 (Borwein and Borwein 1987, pp. 91 and 95), where
(Borwein and Borwein 1987, pp. 91 and 95), where 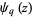 is a q-polygamma function. Special cases and related sums include
is a q-polygamma function. Special cases and related sums include
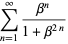 |
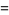 |
![1/4[theta_3^2(beta)-1]](https://mathworld.wolfram.com/images/equations/LambertSeries/Inline22.gif) |
(8) |
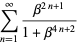 |
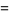 |
![1/4[theta_3^2(beta)-theta_2^2(beta)]](https://mathworld.wolfram.com/images/equations/LambertSeries/Inline25.gif) |
(9) |
 |
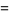 |
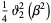 |
(10) |
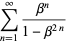 |
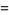 |
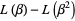 |
(11) |
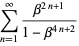 |
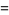 |
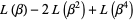 |
(12) |
(Borwein and Borwein 1997, pp. 91-92), which arise in the reciprocal Fibonacci and reciprocal Lucas constants.
Some beautiful series of this type include
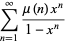 |
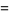 |
 |
(13) |
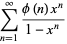 |
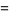 |
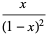 |
(14) |
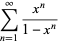 |
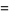 |
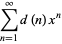 |
(15) |
 |
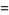 |
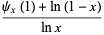 |
(16) |
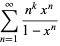 |
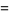 |
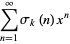 |
(17) |
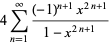 |
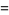 |
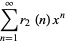 |
(18) |
 |
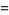 |
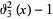 |
(19) |
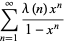 |
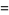 |
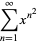 |
(20) |
 |
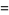 |
![1/2[theta_3(x)-1]](https://mathworld.wolfram.com/images/equations/LambertSeries/Inline61.gif) |
(21) |
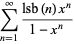 |
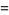 |
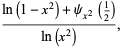 |
(22) |
where 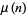 is the Möbius function,
is the Möbius function, 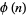 is the totient function,
is the totient function, 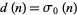 is the number of divisors of
is the number of divisors of 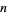 ,
, 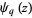 is the q-polygamma function,
is the q-polygamma function, 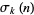 is the divisor function,
is the divisor function, 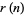 is the number of representations of
is the number of representations of 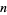 in the form
in the form 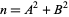 where
where 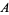 and
and 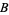 are rational integers (Hardy and Wright 1979),
are rational integers (Hardy and Wright 1979), 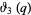 is a Jacobi elliptic function (Bailey et al. 2006),
is a Jacobi elliptic function (Bailey et al. 2006), 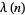 is the Liouville function, and
is the Liouville function, and 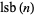 is the least significant bit of
is the least significant bit of 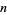 .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Number Theoretic Functions." §24.3.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 826-827, 1972.
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 24-15, 1997.
Arndt, J. "On Computing the Generalized Lambert Series." 24 Jun 2012. https://arxiv.org/abs/1202.6525.
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006.
Borwein, J. M. and Borwein, P. B. "Evaluation of Sums of Reciprocals of Fibonacci Sequences." §3.7 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 91-101, 1987.
Erdős, P. "On Arithmetical Properties of Lambert Series." J. Indian Math. Soc. 12, 63-66, 1948.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 257-258, 1979.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|