


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-1-2021
Date: 28-8-2020
Date: 1-11-2020
|
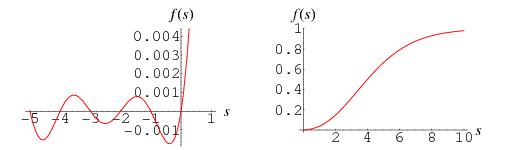
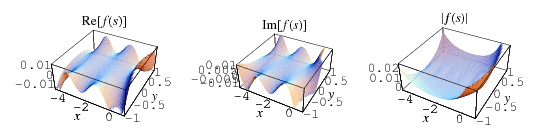
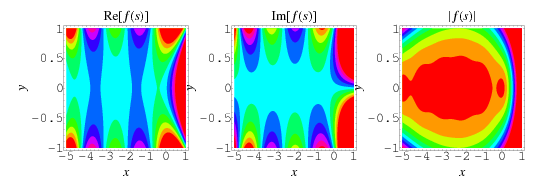
Ramanujan's Dirichlet L-series is defined as
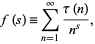 |
(1) |
where 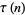 is the tau function. Note that the notation
is the tau function. Note that the notation 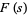 is sometimes used instead of
is sometimes used instead of 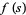 (Hardy 1999, p. 164).
(Hardy 1999, p. 164).
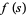 has properties analogous to the Riemann zeta function, and is implemented as RamanujanTauL[s].
has properties analogous to the Riemann zeta function, and is implemented as RamanujanTauL[s].
Ramanujan conjectured that all nontrivial zeros of 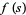 lie on the line
lie on the line ![R[s]=6](https://mathworld.wolfram.com/images/equations/TauDirichletSeries/Inline6.gif) .
.
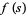 satisfies the functional equation
satisfies the functional equation
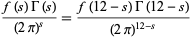 |
(2) |
(Hardy 1999, p. 173) and has the Euler product representation
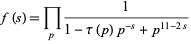 |
(3) |
for ![sigma=R[s]>7](https://mathworld.wolfram.com/images/equations/TauDirichletSeries/Inline8.gif) (since
(since 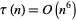 ) (Apostol 1997, p. 137; Hardy 1999, p. 164).
) (Apostol 1997, p. 137; Hardy 1999, p. 164).
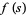 can be split up into
can be split up into
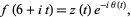 |
(4) |
where
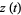 |
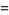 |
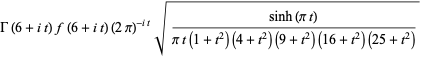 |
(5) |
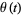 |
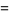 |
![-1/2iln[(Gamma(6+it))/(Gamma(6-it))]-tln(2pi).](https://mathworld.wolfram.com/images/equations/TauDirichletSeries/Inline16.gif) |
(6) |
The functions 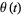 , and
, and 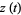 are returned by the Wolfram Language commands RamanujanTauTheta[t] and RamanujanTauZ[t], respectively.
are returned by the Wolfram Language commands RamanujanTauTheta[t] and RamanujanTauZ[t], respectively.
Ramanujan's tau 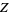 -function
-function 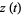 is a real function for real
is a real function for real 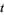 and is analogous to the Riemann-Siegel function
and is analogous to the Riemann-Siegel function 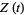 . The number of zeros in the critical strip from
. The number of zeros in the critical strip from 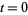 to
to 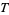 is given by
is given by
![N(t)=(Theta(T)+I{ln[f(6+iT)]})/pi,](https://mathworld.wolfram.com/images/equations/TauDirichletSeries/NumberedEquation5.gif) |
(7) |
where 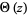 is the Ramanujan theta function. Ramanujan conjectured that the nontrivial zeros of the function are all real.
is the Ramanujan theta function. Ramanujan conjectured that the nontrivial zeros of the function are all real.
Ramanujan's 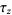 function is defined by
function is defined by
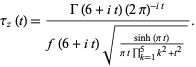 |
(8) |
REFERENCES:
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, 1997.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Keiper, J. "On the Zeros of the Ramanujan  -Dirichlet Series in the Critical Strip." Math. Comput. 65, 1613-1619, 1996.
-Dirichlet Series in the Critical Strip." Math. Comput. 65, 1613-1619, 1996.
Spira, R. "Calculation of the Ramanujan Tau-Dirichlet Series." Math. Comput. 27, 379-385, 1973.
Yoshida, H. "On Calculations of Zeros of L-Functions Related with Ramanujan's Discriminant Function on the Critical Line." J. Ramanujan Math. Soc. 3, 87-95, 1988.



|
|
|
|
حقن الذهب في العين.. تقنية جديدة للحفاظ على البصر ؟!
|
|
|
|
|
|
|
علي بابا تطلق نماذج "Qwen" الجديدة في أحدث اختراق صيني لمجال الذكاء الاصطناعي مفتوح المصدر
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستذكر سيرة السيدة المعصومة (عليها السلام) وسعة علمها ومكانتها
|
|
|