


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-5-2020
Date: 8-2-2020
Date: 8-5-2020
|
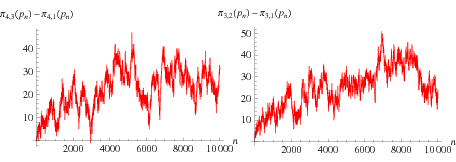
Chebyshev noticed that the remainder upon dividing the primes by 4 gives 3 more often than 1, as plotted above in the left figure. Similarly, dividing the primes by 3 gives 2 more often than 1 (right figure). This is called the Chebyshev bias, or sometimes the prime race (Wagon 1994).
Consider the list of the first  primes
primes  (mod 4). This list contains equal numbers of remainders 3 and 1 (mod 4) for
(mod 4). This list contains equal numbers of remainders 3 and 1 (mod 4) for  , 3, 7, 13, 89, 2943, 2945, 2947, 2949, 2951, 2953, 50371, ... (OEIS A038691; Wagon 1994, pp. 2-3). The values of
, 3, 7, 13, 89, 2943, 2945, 2947, 2949, 2951, 2953, 50371, ... (OEIS A038691; Wagon 1994, pp. 2-3). The values of 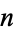 for which the list is biased towards 1 are 2946, 50378, 50380, 50382, 50383, 50384, 50385, ... (OEIS A096628).
for which the list is biased towards 1 are 2946, 50378, 50380, 50382, 50383, 50384, 50385, ... (OEIS A096628).
Defining
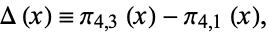 |
the values of 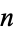 for which
for which 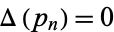 are
are 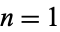 , 3, 7, 13, 89, 2943, 2945, 2947, ... (OEIS A038691).
, 3, 7, 13, 89, 2943, 2945, 2947, ... (OEIS A038691).
Similarly, consider the list of the first 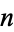 primes
primes 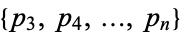 (mod 3), skipping
(mod 3), skipping 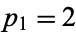 and
and 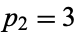 since
since 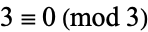 . This list contains equal numbers of remainders 2 and 1 at the values
. This list contains equal numbers of remainders 2 and 1 at the values 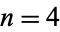 , 6, 8, 12, 14, 22, 38, 48, 50, ... (OEIS A096629). The first value of
, 6, 8, 12, 14, 22, 38, 48, 50, ... (OEIS A096629). The first value of 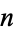 for which the list is biased towards 1 is
for which the list is biased towards 1 is 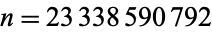 , as first found by Bays and Hudson in 1978 (Derbyshire 2004, p. 126), giving the first few such values as 23338590792, 23338590794, 23338590795, 23338590796, ... (OEIS A096630).
, as first found by Bays and Hudson in 1978 (Derbyshire 2004, p. 126), giving the first few such values as 23338590792, 23338590794, 23338590795, 23338590796, ... (OEIS A096630).
REFERENCES:
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 125-126, 2004.
Sloane, N. J. A. Sequences A038691, A096628, A096629, and A096630 in "The On-Line Encyclopedia of Integer Sequences."
Wagon, S. The Power of Visualization. Front Range Press, 1994.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
مجمع العفاف النسوي: مهرجان تيجان العفاف يعزز القيم الأخلاقية والثقافية لدى طالبات الجامعات العراقية
|
|
|