Kennedy and Levins aspectual account Evaluation

From the present perspective, the central question is to what extent Kennedy and Levin’s account includes an analysis of aspectual composition in terms of gradability. Alternatively, to recall their claim to what extent does quantization/telicity follow completely from the structure of the degree of change argument? At first glance, their account seems to fare well, because the characterizations appear unobjectionable. However it is also desirable for an aspectual theory to derive these results, and here their account leaves something to be desired.

Consider how the following two telic VPs (ignoring the in-PPs) might be derived in Kennedy and Levin’s framework:

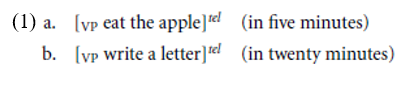
Beginning with (1a), since the definite object NP the apple may be treated as a term, the meaning of eat can be applied to the meaning of the apple:¹

A technical issue with the result in (2c) is that the degree argument has not yet been discharged. Allowing for a default mechanism of existential binding of the degree argument at the VP level (as Kennedy and Levin in fact do), we obtain the following event predicate:

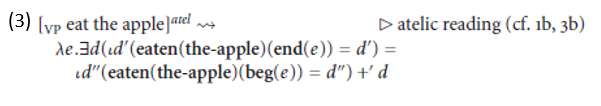
Observe that this event predicate is cumulative as long as it is non-unique: the events in its denotation are events in which some amount d of the apple is eaten, and the sum of any two of these is also an event in which some (larger) amount d of the apple is eaten. This corresponds to the atelic reading of the VP.

Even so, the issue is still how to derive the telic interpretion of (1a), for which there appear to be two potential strategies. The first would be to have the degree of change argument remain free within the VP, because this would yield a quantized event predicate:

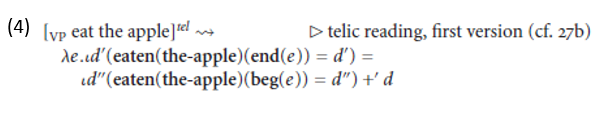
Although this event predicate is indeed quantized, it does not capture the intuitive meaning of the VP, because the events denoted in (4) are those in which d-much of the apple is eaten, for a fixed value of d, but nothing forces the value of d to be maximal (or nearly maximal, allowing for a certain vagueness). Yet, intuitively, the meaning of the VP applies to events in which the apple is wholly eaten. Consequently, the first potential strategy, according to which the degree argument is free and implicitly specified, as in (4), would be in general too weak.²

The second strategy would be to set the value of the degree of change to be maximal, which would yield the interpretation on which all of the apple is eaten. Technically, Kennedy and Levin treat eaten as a “negative property,” which means that its possible values are negative degrees. Furthermore, although Kennedy and Levin do not state this explicitly, the scale defined by eaten is evidently closed. Consequently, degrees of “being eaten” have the form [p, 1], for a choice of p, and the maximal negative degree is [0, 1]. In order to get this as the result, the value of the degree of change (which is always a positive degree) should also be set to [0, 1]:³

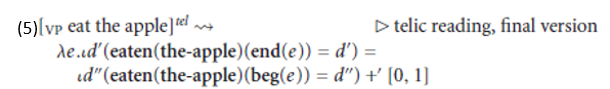
Since the degree of change in (5) is specified as [0, 1], it follows that the degree to which the apple is eaten at the beginning of an event in the denotation of this predicate is [1, 1] (or 1), which is the minimal negative degree. In other words, none of the apple is eaten at the beginning of such an event, and it is fully eaten by the end.

Although the second strategy would yield the desired result, it is a bit unclear how to obtain it in Kennedy and Levin’s framework. More precisely, how does d, which is an argument of the verb, get specified as [0, 1]? More generally, if the value of d is not explicitly specified, Kennedy and Levin suggest that it may be inferred on the basis of the lexical semantics of the verb or its arguments, or even on the basis of extralinguistic knowledge. In the case of (2c), then, the idea seems to be that since the apple is quantized, it is natural to infer that the value of d is maximal. However, unless more is said about how this inference mechanism works in conjunction with representations like that in (2c), the account is lacking something.

The telic VP in (1b) poses the same problem, though here the object NP is indefinite. If a letter is analyzed as a generalized quantifier, as in (6b), it can apply to the meaning of write in (6a) to yield the relation between events and degrees in (6c).

As before, the problem is how to discharge d and to restrict its value to be maximal in the absence of an explicit degree expression. Moreover, as seen earlier in connection with (3), it would not suffice simply to existentially bind d at the VP level, because this would yield an atelic VP.

Suppose that we have a mechanism for setting the degree of change to be maximal. Then nothing would restrain it from applying in the case of atelic VPs, illustrated in (7).

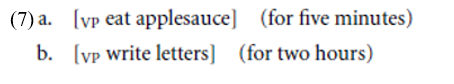
Consider how the VP in (7a) might be derived, treating the object NP apple- sauce as a generalized quantifier:

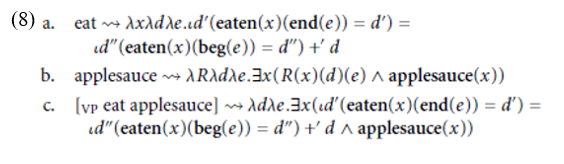
Given the relation between events e and degrees d in (8c), one possibility would be to existentially bind d at the VP level

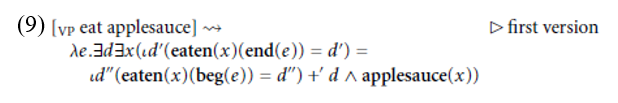
This event predicate is cumulative (provided that it is non-unique), hence this analysis would successfully capture the fact that the VP eat applesauce is atelic. In prose, this predicate denotes events in which some amount d of some applesauce is eaten, and the sum of any two such events is also an event in which some (greater) amount d of some (greater quantity of) applesauce is eaten. However, once a mechanism for fixing the value of d to be [0, 1] is available, it could apply to the relation in (37c) to yield the following event predicate (cf. 5):

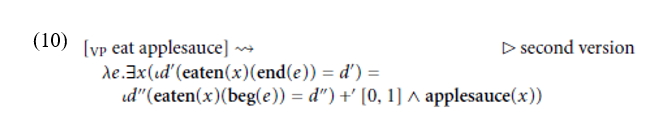
Perhaps somewhat surprisingly, this event predicate is also cumulative (provided that it is non-unique): it denotes events in which some applesauce is maximally eaten, but the sum of any two events in which some applesauce is maximally eaten is also an event in which some (greater quantity of) applesauce is maximally eaten. Of course, the quantity of applesauce is not held constant here, but nor does it have to be, given that x is existentially bound in (10).

The contrast between the event predicate in (5), which is quantized (telic) and specifies a maximal degree of change, on the one hand, and the event predicate in (10), which is cumulative (atelic) and specifies a maximal degree of change, on the other, sharply demonstrates that quantization/telicity does not follow completely from the structure of the degree of change argument, contrary to Kennedy and Levin’s initial claim. Clearly, the choice of object NP is a crucial factor here.⁴ In the case of the apple, which is quantized, the way in which the degree of change is specified does matter, as seen in the contrast between (3) (cumulative, atelic) and (5) (quantized, telic). However, in the case of applesauce, which is cumulative, the way in which the degree of change is specified does not matter, as witnessed in the lack of contrast between (9) and (10) (both cumulative, atelic).

The same issue arises for the atelic VP in (7b), which contains the cumulative object NP letters. No matter how the degree of change is specified, the corresponding event predicate is cumulative, which differs from the VP in (6c) with the quantized objectNP a letter, for here the way in which the degree of change is specified does determine whether the VP is telic or atelic. In sum, Kennedy and Levin’s account does not quite succeed in offering an analysis of aspectual composition in terms of gradability, contrary to initial claims and appearances, because it does not relate the value of the degree of change argument to the quantized/cumulative character of the object NP.

1 For present purposes, nothing depends on whether the apple is analyzed as a term, a predicate (namely, Îx.x = the-apple), or even a generalized quantifier. Accordingly, nothing requires the verb to be treated as a functor for the object NP – cf. (35) below.

2 Note that this is not a problem in the case of degree achievements. For example, the meaning of lengthen the rope (cf. 27a) does not require the degree of change d to be maximal – indeed, given that the scale of length is closed at 0 and open at 1 (cf. 15), d could not have a maximal value anyway.

3 Then the first clause in (14) would apply, where d is [1, 1] (the minimal negative degree) and d is [0, 1] (the maximal positive degree of change), therefore d +               d            = [1, 1] +              [0, 1] = [0, 1] (the maximal negative degree).

4 Rothstein (2004: 118) makes a similar point in a critique of Kennedy and Levin (2002) based on examples such as The tailor lengthened skirts five centimeters for three months, claiming that Kennedy and Levin’s account is not a theory of telicity. Although I basically agree with Rothstein on this point (though it is perhaps arguable whether Kennedy and Levin really promised a “theory of telicity”), it is also evident that she has little sympathy for a degree-based account to begin with, given her own non-degree-based approach to promote. Furthermore, as far as I can tell, she does not actually show how degree achievements would be treated in her framework.