المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Roth,s Theorem |
 560
 03:07 مساءً
date: 17-10-2020 |
Author : Cassels, J. W. S. 
Book or Source : An Introduction to Diophantine Approximations. Cambridge, England: Cambridge University Press, 1957. 
Page and Part : ...|
Read More
Date: 30-7-2020
1666
Date: 3-8-2020
671
Date: 6-9-2020
1084
|
For algebraic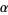 
 |
with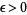 
, has finitely many solutions. Klaus Roth received a Fields medal for this result.
REFERENCES:
Cassels, J. W. S. An Introduction to Diophantine Approximations. Cambridge, England: Cambridge University Press, 1957.
Davenport, H. and Roth, K. F. "Rational Approximations to Algebraic Numbers." Mathematika 2, 160-167, 1955.
Roth, K. F. "Rational Approximations to Algebraic Numbers." Mathematika 2, 1-20, 1955.
Roth, K. F. "Corrigendum to 'Rational Approximations to Algebraic Numbers.' " Mathematika 2, 168, 1955.
|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|
