


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-1-2021
Date: 14-1-2020
Date: 30-9-2020
|
The Ulam sequence 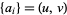 is defined by
is defined by 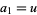 ,
, 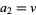 , with the general term
, with the general term 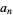 for
for 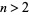 given by the least integer expressible uniquely as the sum of two distinct earlier terms. The numbers so produced are sometimes called u-numbers or Ulam numbers.
given by the least integer expressible uniquely as the sum of two distinct earlier terms. The numbers so produced are sometimes called u-numbers or Ulam numbers.
The first few numbers in the (1, 2)-Ulam sequence are 1, 2, 3, 4, 6, 8, 11, 13, 16, ... (OEIS A002858). Here, the first term after the initial (1, 2) is obviously 3 since 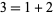 . The next term is
. The next term is 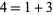 . (We don't have to worry about
. (We don't have to worry about 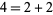 since it is a sum of a single term instead of distinct terms.) 5 is not a member of the sequence since it is representable in two ways,
since it is a sum of a single term instead of distinct terms.) 5 is not a member of the sequence since it is representable in two ways, 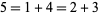 , but
, but 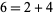 is a member.
is a member.
Proceeding in the manner, we can generate Ulam sequences for any 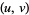 , examples of which are given in the table below.
, examples of which are given in the table below.
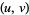 |
Sloane | sequence |
| (1, 2) | A002858 | 1, 2, 3, 4, 6, 8, 11, 13, 16, 18, ... |
| (1, 3) | A002859 | 1, 3, 4, 5, 6, 8, 10, 12, 17, 21, ... |
| (1, 4) | A003666 | 1, 4, 5, 6, 7, 8, 10, 16, 18, 19, ... |
| (1, 5) | A003667 | 1, 5, 6, 7, 8, 9, 10, 12, 20, 22, ... |
| (2, 3) | A001857 | 2, 3, 5, 7, 8, 9, 13, 14, 18, 19, ... |
| (2, 4) | A048951 | 2, 4, 6, 8, 12, 16, 22, 26, 32, 36, ... |
| (2, 5) | A007300 | 2, 5, 7, 9, 11, 12, 13, 15, 19, 23, ... |
Schmerl and Spiegel (1994) proved that Ulam sequences 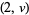 for odd
for odd 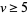 have exactly two even terms. Ulam sequences with only finitely many even terms eventually must have periodic successive differences (Finch 1991, 1992abc). Cassaigne and Finch (1995) proved that the Ulam sequences
have exactly two even terms. Ulam sequences with only finitely many even terms eventually must have periodic successive differences (Finch 1991, 1992abc). Cassaigne and Finch (1995) proved that the Ulam sequences 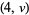 for
for 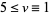 (mod 4) have exactly three even terms.
(mod 4) have exactly three even terms.
The Ulam sequence can be generalized by the s-additive sequence.
REFERENCES:
Cassaigne, J. and Finch, S. "A Class of 1-Additive Sequences and Quadratic Recurrences." Exper. Math 4, 49-60, 1995.
Finch, S. "Conjectures About 1-Additive Sequences." Fib. Quart. 29, 209-214, 1991.
Finch, S. "Are 0-Additive Sequences Always Regular?" Amer. Math. Monthly 99, 671-673, 1992a.
Finch, S. "On the Regularity of Certain 1-Additive Sequences." J. Combin. Th. Ser. A 60, 123-130, 1992b.
Finch, S. "Patterns in 1-Additive Sequences." Exper. Math. 1, 57-63, 1992c.
Finch, S. R. "Stolarsky-Harborth Constant." §2.16 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 145-151, 2003.
Guy, R. K. "A Quarter Century of Monthly Unsolved Problems, 1969-1993." Amer. Math. Monthly 100, 945-949, 1993.
Guy, R. K. "Ulam Numbers." §C4 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 109-110, 1994.
Guy, R. K. and Nowakowski, R. J. "Monthly Unsolved Problems, 1969-1995." Amer. Math. Monthly 102, 921-926, 1995.
Recaman, B. "Questions on a Sequence of Ulam." Amer. Math. Monthly 80, 919-920, 1973.
Schmerl, J. and Spiegel, E. "The Regularity of Some 1-Additive Sequences." J. Combin. Theory Ser. A 66, 172-175, 1994.
Sloane, N. J. A. Sequences A001857/M0634, A002858/M0557, A002859/M2303, A003666/M3237, A003667/M3746, and A007300/M1328 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 908, 2002.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|