


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-6-2020
Date: 29-11-2020
Date: 13-2-2020
|
A number 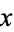 in which the first
in which the first 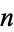 decimal digits of the fractional part
decimal digits of the fractional part 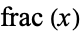 sum to 666 is known as an evil number (Pegg and Lomont 2004).
sum to 666 is known as an evil number (Pegg and Lomont 2004).

However, the term "evil" is also used to denote nonnegative integers that have an even number of 1s in their binary expansions, the first few of which are 0, 3, 5, 6, 9, 10, 12, 15, 17, 18, 20, ... (OEIS A001969), illustrated above as a binary plot. Numbers that are not evil are then known as odious numbers.
Returning to Pegg's definition of evil, the fact that 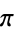 is evil was noted by Keith, while I. Honig (pers. comm., May 9, 2004) noted that the golden ratio
is evil was noted by Keith, while I. Honig (pers. comm., May 9, 2004) noted that the golden ratio 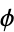 is also evil. The following table gives a list of some common evil numbers (Pegg and Lomont 2004).
is also evil. The following table gives a list of some common evil numbers (Pegg and Lomont 2004).
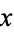 |
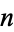 |
Ramanujan constant 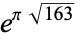 |
132 |
hard hexagon entropy constant 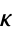 |
137 |
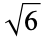 |
139 |
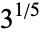 |
140 |
Stieltjes constant 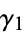 |
142 |
pi 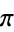 |
144 |
golden ratio 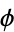 |
146 |
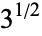 |
146 |
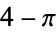 |
151 |
Glaisher-Kinkelin constant 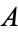 |
153 |
| cube line picking average length | 155 |
Delian constant 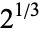 |
156 |
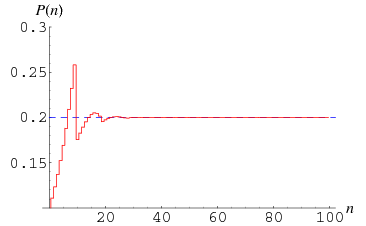
The probability of the digits of a given real number summing to a relatively large positive integer is roughly given by the number of nonzero digits divided by sum of those digits, namely 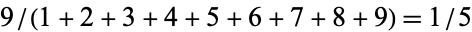 . Amazingly, the exact probability for summing to a number
. Amazingly, the exact probability for summing to a number 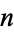 can be computed exactly using the recursive formulas
can be computed exactly using the recursive formulas
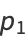 |
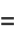 |
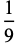 |
(1) |
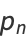 |
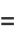 |
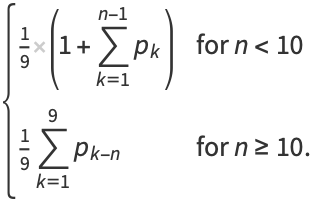 |
(2) |
For 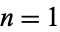 , 2, ..., the first few values are therefore 1/9, 10/81, 100/739, 1000/6561, ... (OEIS A100061 and A100062; Pegg and Lomont 2004), plotted above.
, 2, ..., the first few values are therefore 1/9, 10/81, 100/739, 1000/6561, ... (OEIS A100061 and A100062; Pegg and Lomont 2004), plotted above.
The generating function for this series is given by
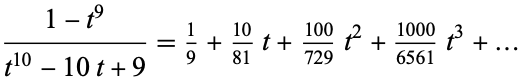 |
(3) |
(Pegg and Lomont 2004). This allows an expression for 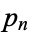 to be determined in closed form, although it is a complicated expression involving combinations of the algebraic numbers (and polynomial roots)
to be determined in closed form, although it is a complicated expression involving combinations of the algebraic numbers (and polynomial roots) 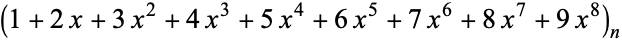 .
.
For the case of interest (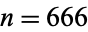 ), the result is a rational number having a 635-digit numerator and a 636-digit denominator that is approximately equal to
), the result is a rational number having a 635-digit numerator and a 636-digit denominator that is approximately equal to
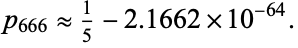 |
(4) |
A set of "beastly evil" numbers are given by the following (M. Hudson, pers. comm., Nov 5-10, 2004).
| number | digits |
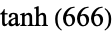 |
74 |
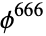 |
74 |
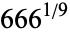 |
136 |
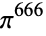 |
142 |
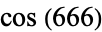 |
146 |
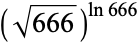 |
147 |
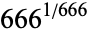 |
149 |
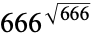 |
152 |
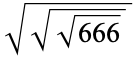 |
156 |
 |
159 |
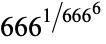 |
163 |
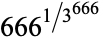 |
468 |
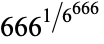 |
655 |
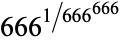 |
2018 |
Powers of 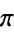 that are evil include
that are evil include 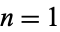 , 6, 8, 10, 17, 18, 24, 25, 26, 29, 30, 38, ... (M. Hudson, pers. comm., Nov. 8, 2004).
, 6, 8, 10, 17, 18, 24, 25, 26, 29, 30, 38, ... (M. Hudson, pers. comm., Nov. 8, 2004).
The analogous problem of terms in a simple continued fraction summing to a given number can also be considered. The following table summarized some constants whose continued fractions have cumulative sums that equal 666 (Pegg and Lomont 2004).
| constant | terms |
| cube line picking average length | 50 |
pi 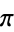 |
56 |
| Bloch constant | 58 |
| Gauss's constant | 143 |
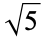 |
167 |
| conjectured value of Landau constant | 173 |
Interestingly, this makes the cube line picking average length and 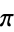 doubly evil.
doubly evil.
REFERENCES:
Keith, M. "The Number of the Beast." https://users.aol.com/s6sj7gt/mike666.htm.
Pegg, E. Jr. and Lomont, C. "Math Games: Evil Numbers." Oct. 4, 2004. https://www.maa.org/editorial/mathgames/mathgames_10_04_04.html.
Sloane, N. J. A. Sequences A001969, A100061 and A100062 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|