


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-9-2020
Date: 16-7-2020
Date: 20-11-2019
|
A positive integer which is divisible by the sum of its digits, also called a Niven number (Kennedy et al. 1980) or a multidigital number (Kaprekar 1955). The first few are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 18, 20, 21, 24, ... (OEIS A005349). Grundman (1994) proved that there is no sequence of more than 20 consecutive Harshad numbers, and found the smallest sequence of 20 consecutive Harshad numbers, each member of which has 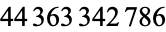 digits.
digits.
Grundman (1994) defined an 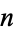 -Harshad (or
-Harshad (or 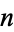 -Niven) number to be a positive integer which is divisible by the sum of its digits in base
-Niven) number to be a positive integer which is divisible by the sum of its digits in base 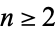 . Cai (1996) showed that for
. Cai (1996) showed that for 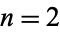 or 3, there exists an infinite family of sequences of consecutive
or 3, there exists an infinite family of sequences of consecutive 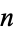 -Harshad numbers of length
-Harshad numbers of length 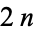 .
.
Define an all-Harshad (or all-Niven) number as a positive integer which is divisible by the sum of its digits in all bases 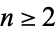 . Then only 1, 2, 4, and 6 are all-Harshad numbers.
. Then only 1, 2, 4, and 6 are all-Harshad numbers.
REFERENCES:
Cai, T. "On 2-Niven Numbers and 3-Niven Numbers." Fib. Quart. 34, 118-120, 1996.
Cooper, C. N. and Kennedy, R. E. "Chebyshev's Inequality and Natural Density." Amer. Math. Monthly 96, 118-124, 1989.
Cooper, C. N. and Kennedy, R. "On Consecutive Niven Numbers." Fib. Quart. 21, 146-151, 1993.
Grundman, H. G. "Sequences of Consecutive 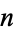 -Niven Numbers." Fib. Quart. 32, 174-175, 1994.
-Niven Numbers." Fib. Quart. 32, 174-175, 1994.
Kaprekar, D. R. "Multidigital Numbers." Scripta Math. 21, 27, 1955.
Kennedy, R. E. and Cooper, C. N. "On the Natural Density of the Niven Numbers." Abstract 816-11-219, Abstracts Amer. Math. Soc. 6, 17, 1985.
Kennedy, R.; Goodman, R.; and Best, C. "Mathematical Discovery and Niven Numbers." MATYC J. 14, 21-25, 1980.
Sloane, N. J. A. Sequence A005349/M0481 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. "Niven Numbers." §2.3 in Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 19 and 28-31, 1991.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 171, 1986.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|