


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-11-22
التاريخ: 2023-12-07
التاريخ: 2023-07-27
التاريخ: 12-2-2022
|
تقريب Wentzel, Kramers, Brillouin WKB
تبدأ من المعادلة التالية:
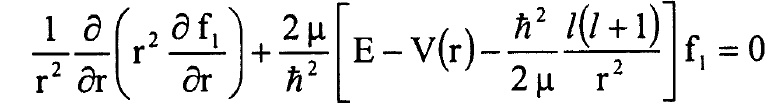
وبعد التعويض فيها بالدالة الموجية Ψ = rf1 نصل الى المعادلة:
 ...............(1)
...............(1)
حيث للجزيئة المهتزة الدوارة:
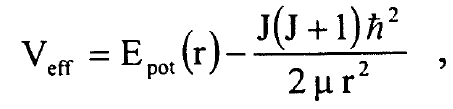 ...............(2)
...............(2)
والطاقة الحركية للحركة النصف قطرية تساوي:
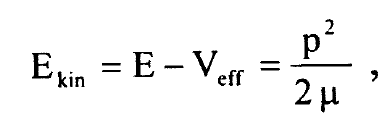 .............(3)
.............(3)
ويمكن التعبير عنها من خلال الزخم النصف قطري:
 ..............(4)
..............(4)
وبتعويض 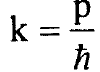 نصل الى المعادلة:
نصل الى المعادلة:
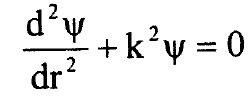 ...............(5)
...............(5)
لجهد ثابت فان k = k0 ويساوي ثابت والمعادلة (5) تصف جسيم حر وحل المعادلة (5) يكون بالدالة:
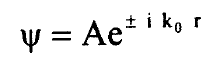 .............(6)
.............(6)
فيمكن تجربة الحل الاتي: r يتغير ببطء مع تغيير V(r) واذا كان
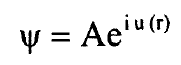 ..........(7)
..........(7)
وبتعويض المعادلة (5) نحصل على معادلة الدالة المجهولة u(r):
 ............(8)
............(8)
واذا كان الجهد لا يتغير بسرعة مع r فان المشتقة الثانية 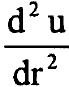 مقدارها قليل ويمكن اهمالها ونحصل على التقريب الصفري u0(r) من المعادلة (8):
مقدارها قليل ويمكن اهمالها ونحصل على التقريب الصفري u0(r) من المعادلة (8):
 .............(9)
.............(9)
وبعد تعويض هذه النتيجة في المعادلة (8) نحصل على التقريب الاول:
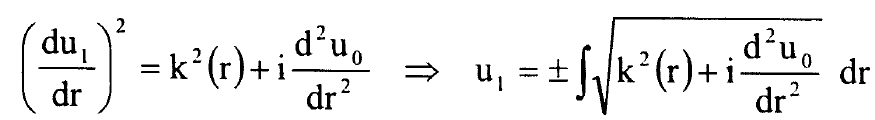 ................(10)
................(10)
هذه المعادلة يمكن استخدامها كأساس لطريقة تقريبية تكرارية حيث يمكن ادخال التقريب (n-1) على يمين المعادلة (10) ونحصل على اقتريب n للدالة u(r) على يسار المعادلة والحلول هي:
 ...............(11)
...............(11)
حيث cn ثابت التكامل ويتعين بالشروط الحدودية وللتقريب الاول نحصل على:
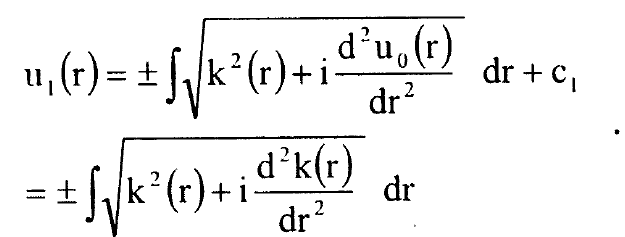 ...........(12)
...........(12)
يتقارب الاجراء اذا كان  وبالتعبير عن المقدار داخل التكامل بمتوالية تصل الى:
وبالتعبير عن المقدار داخل التكامل بمتوالية تصل الى:
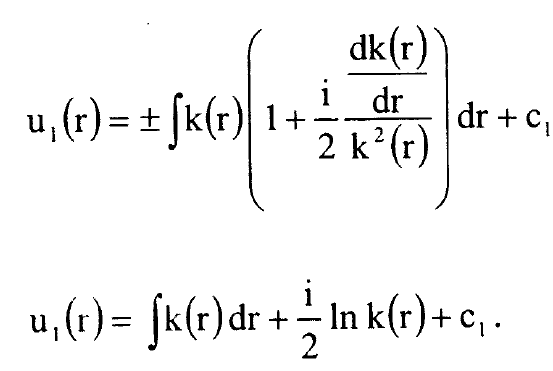 ............(13)
............(13)
للدالة الموجية (Ψ(r نحصل على الحل التقريبي:
 ............(14)
............(14)
وهو المعروف بتقريب WKB وبإدخال طول موجة دي برولي 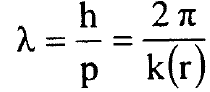 يمكن كتابة معيار التقارب
يمكن كتابة معيار التقارب  بالشكل:
بالشكل:
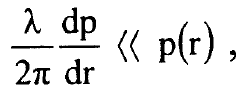 .................(15)
.................(15)
اي ان التقريب صحيح اذا كان تغير الزخم خلال طول موجية واحد من موجة دي برولي صغير بالنسبة الى الزخم نفسه.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
قسم الشؤون الفكرية يصدر كتاب الفلسفة الغربية برؤية الشيخ مرتضى مطهري
|
|
|