


 المحاسبة
المحاسبة 
 ادارة الاعمال
ادارة الاعمال
 الادارة
الادارة
 وظيفة التخطيط
وظيفة التخطيط 
 وظيفة التنظيم
وظيفة التنظيم
 وظيفة التوجيه
وظيفة التوجيه 
 وظيفة الرقابة
وظيفة الرقابة 
 ادارة الانتاج
ادارة الانتاج
 ادارة الجودة
ادارة الجودة 
 الادارة الاستراتيجية
الادارة الاستراتيجية
 ادارة التسويق
ادارة التسويق
 ادارة الموارد البشرية
ادارة الموارد البشرية 
 علوم مالية و مصرفية
علوم مالية و مصرفية
 المالية العامة
المالية العامة 
 الاقتصاد
الاقتصاد
 الأحصاء
الأحصاء|
أقرأ أيضاً
التاريخ: 2023-06-09
التاريخ: 2023-05-30
التاريخ: 2023-12-25
التاريخ: 2023-12-25
|
4 - 1 - 2 - 9 - 3 أسلوب خط الاتجاه Trend Line Method
يعد هذا الأسلوب من الأساليب الشائعة الاستخدام في تنبؤ الطلب على المنتجات. وتفترض هذه الطريقة إن الطلب على المنتجات يتغير (يزيد أو ينقص ) بمرور الزمن، وان ما حدث للطلب في الماضي يمكن ان يتكرر في المستقبل. وتستخدم معادلة خط الاتجاه العام لتقدير الطلب في المستقبل. ويعبر عن هذه المعادلة بالصيغة الأتية :

ويتم حساب ثوابت معادلة (3ــ9) باستخدام البيانات المتوفرة عن السلسلة الزمنية بحيث إذا ما رسمت هذه المعادلة فوق نفس البيانات كما في الشكل (3ـ 9) فان الشروط التالية سوف تحقق:
أ ـ مجموع الانحرافات العمودية بين أي نقطة على الرسم و النقطة التي تقابلها على خط الاتجاه يساوي صفرا .
ب ـ مجموع مربع الانحرافات العمودية بين أي نقطة على الرسم و النقطة المقترنة بها على خط الاتجاه يكون أصغر ما يمكن.
ج - خط الاتجاه يمر في الوسط الحسابي البيانات .
وعلى افتراض ان معادلة الاتجاه ذات صيغة خطية، فان ثوابت معادلة خط الاتجاه تُحسب عن طريق حل المعادلتين الطبيعيتين (Normal Equations) التاليتين بطريقة آنية :
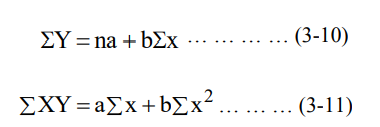
حيث إن: n= عدد المشاهدات في السلسلة الزمنية
ولحل المعادلتين السابقتين فإننا نجد الوسط الفرضي للمتغير (X) أولا، ثم نقوم بطرح قيمة الوسط الفرضي من قيم المتغير (X) وجمع النتائج فيكون حاصل جمع الفرق مساوياً إلى صفر 0 = X£. ويجعل في معادلتي (3-10) (3 ــ 11) تحصل على الصيغة التالية:
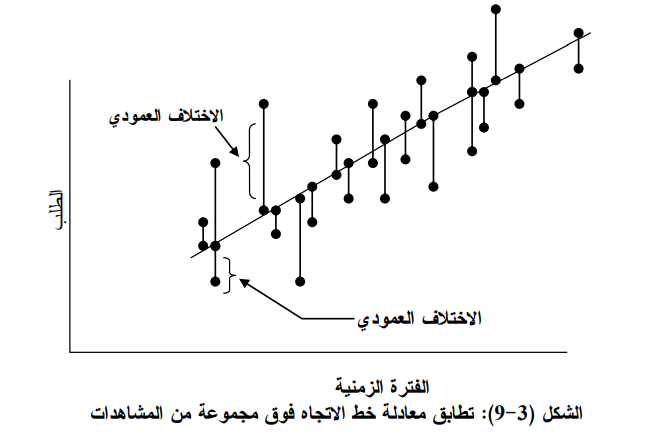
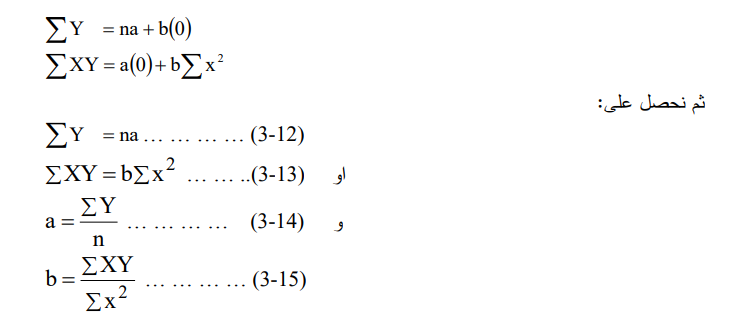
والمثال التالي يوضح كيفية تطبيق هذه الطريقة :
مثال 3 ـ5 :
الجدول التالي يبين الطلب على إطارات السيارات من قياس 175 × 13 لدى احدى شركات استيراد وتوزيع الإطارات للأعوام 1999 – 2009 والمطلوب إعداد معادلة خط الاتجاه وتنبؤ الطلب لعام 2010 و 2011 .
الحل /
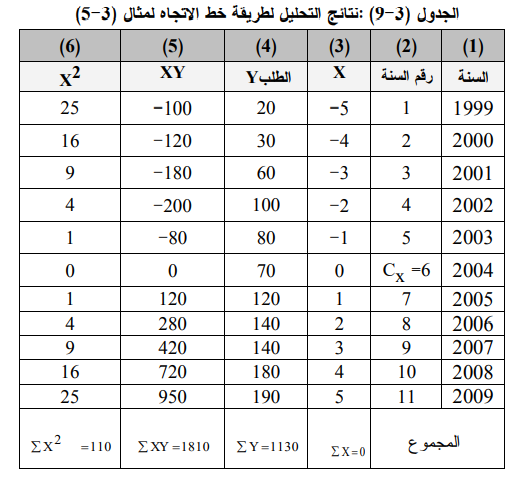
1ـ نقوم بترقيم السنوات من 1999- 2009 وكما يظهر في الجدول (3-9) عمود (2) .
2ـ نجد قيمة الوسط الفرضي (او المركز) للسلسلة X بالقاعدة الآتية:

3ـ نطرح من رقم كل سنة قيمة الوسط الفرضي فنحصل على النتائج المبينة في الجدول (3-9) عمود (3) .
4ـ نعوض القيم التي حصلنا من الجدول (3-9) في معادلتي (3-10) و(3-11) فنحصل على قيمة a , b كالآتي :
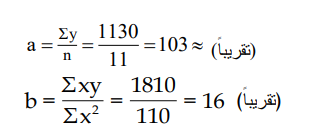
وعلى هذا الاساس فإن معادلة التنبؤ لمثالنا تُكتب بالصيغة التالية :
Y = 103 +16X
وبما ان السنة 2010 والسنة 2011 ستحصلان على رقم 12 و13 على التوالي في السلسلة X فإن تنبؤ الطلب لسنة 2010 يُحسب كالآتي :

إن الرقم 6 الذي حل محل X لا يشير إلى مركز السلسلة X ، وإنما يشير إلى عدد السنوات التي تفرق بين سنة 2010 ومركز السلسلة x الذي يقابل سنة 2004 أي (6 = 2004 - 2010) أو (6 = 6 - 12). وبالنسبة لعام 2011 فان هذا الفرق يبلغ (7) أي (7 =6 - 13).
أما التنبؤ لسنة 2001 فانه يبلغ:
Y13 = 103 + 16(7)
أو 215000 لأن الطلب بالآلاف 215 =
ويمتاز هذا الأسلوب بأنه يأخذ جميع المشاهدات بنظر الاعتبار عند استخراج ثوابت المعادلة الأمر الذي يقلل من اثر العوامل العشوائية. ويعاب عليه بأنه يتطلب مجهوداً حسابياً مطولاً، فضلاً عن أنه يعطي نفس الوزن أو الأهمية لجميع المشاهدات كما انه غير قادر على تحسس الآثار الموسمية التي تؤثر في الطلب.



|
|
|
|
تحذير من "عادة" خلال تنظيف اللسان.. خطيرة على القلب
|
|
|
|
|
|
|
دراسة علمية تحذر من علاقات حب "اصطناعية" ؟!
|
|
|
|
|
|
|
شركة اللواء العالمية تعرض منتجاتها في الأسبوع الزراعي السادس عشر في بغداد
|
|
|