


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-2-2020
Date: 24-10-2020
Date: 10-10-2020
|
A Poulet number is a Fermat pseudoprime to base 2, denoted psp(2), i.e., a composite number 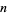 such that
such that
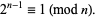 |
The first few Poulet numbers are 341, 561, 645, 1105, 1387, ... (OEIS A001567).
Pomerance et al. (1980) computed all 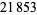 Poulet numbers less than
Poulet numbers less than 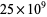 . The numbers less than
. The numbers less than 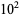 ,
, 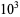 , ..., are 0, 3, 22, 78, 245, ... (OEIS A055550).
, ..., are 0, 3, 22, 78, 245, ... (OEIS A055550).
Pomerance has shown that the number of Poulet numbers less than  for sufficiently large
for sufficiently large  satisfy
satisfy
![exp[(lnx)^(5/14)]<P_2(x)<xexp(-(lnxlnlnlnx)/(2lnlnx))](https://mathworld.wolfram.com/images/equations/PouletNumber/NumberedEquation2.gif) |
(Guy 1994).
A Poulet number all of whose divisors 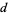 satisfy
satisfy 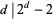 is called a super-Poulet number. There are an infinite number of Poulet numbers which are not super-Poulet numbers. Shanks (1993) calls any integer satisfying
is called a super-Poulet number. There are an infinite number of Poulet numbers which are not super-Poulet numbers. Shanks (1993) calls any integer satisfying 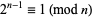 (i.e., not limited to odd composite numbers) a Fermatian.
(i.e., not limited to odd composite numbers) a Fermatian.
REFERENCES:
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 28-29, 1994.
Pinch, R. G. E. "The Pseudoprimes Up to 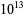 ." ftp://ftp.dpmms.cam.ac.uk/pub/PSP/.
." ftp://ftp.dpmms.cam.ac.uk/pub/PSP/.
Pomerance, C.; Selfridge, J. L.; and Wagstaff, S. S. Jr. "The Pseudoprimes to 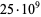 ." Math. Comput. 35, 1003-1026, 1980. http://mpqs.free.fr/ThePseudoprimesTo25e9.pdf.
." Math. Comput. 35, 1003-1026, 1980. http://mpqs.free.fr/ThePseudoprimesTo25e9.pdf.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 115-117, 1993.
Sloane, N. J. A. Sequences A001567/M5441 and A055550 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
بالفيديوغراف: ممثل المرجعية العليا والأمين العام للعتبة الحسينية يتفقدان مشروع مطار كربلاء الدولي
|
|
|