
المفاضلة بين بدائل العمليات أو أنظمة الإنتاج
 المؤلف:
د . عبد الكريم محسن د . صباح مجيد النجار
المؤلف:
د . عبد الكريم محسن د . صباح مجيد النجار
 المصدر:
ادارة الانتاج والعمليات
المصدر:
ادارة الانتاج والعمليات
 الجزء والصفحة:
ص224-227
الجزء والصفحة:
ص224-227
 27-1-2021
27-1-2021
 6051
6051
6 - 5 المفاضلة بين بدائل العمليات أو أنظمة الإنتاج
تتوفر أساليب كمية عديدة يمكن أن تُستخدم في إختيار نوع نظام الإنتاج. ومن بين تلك الأساليب ذلك الذي تستند قواعد القرار فيه على مفاضلة أو مبادلة الكلفة المرتبطة بحجم الطلب على المنتوج، وهو تحليل مستوى التعادل الذي تحدثنا عنه في الفصل الرابع. يعتبر تحليل مستوى التعادل بیانية ورياضية مفيدة في تقويم المستويات المختلفة من الأتمتة في نظم العمليات. إن العمليات أو نظم الإنتاج الأكثر أتمتة تكون تكاليفها الثابتة مرتفعة وتكاليفها المتغيرة منخفضة، لذلك يعتمد إختيار نظام الإنتاج الأفضل على حجم الطلب المتوقع على المنتوج أو المنتجات التي ستُنتج والمفاضلة بين البدائل على اساس التكاليف الكلية للانتاج.
يساعد تحليل مستوى التعادل في المقارنة بين البدائل على أساس اقتصادي وذلك بتحديد العلاقة بين التكاليف الثابتة والتكاليف المتغيرة من خلال صياغة معادلة التكاليف الكلية للبديل. وبتطبيق هذا الأسلوب بیانياً ينبغي إتباع الخطوات الاتية :
1ـ تحديد التكاليف الثابتة المقترنة بكل بديل .
2ـ تحديد التكاليف المتغيرة المقترنة بإنتاج الوحدة الواحدة للمنتوج .
3ـ إعداد معادلات الكلفة الكلية لكل بديل على وفق الصيغة الأتية :
TC =F+VQ ... ... ...(4-1)
إذ إن TC = التكاليف الكلية لعملية الإنتاج أو نظام الإنتاج .
F = التكاليف الثابتة.
V = التكاليف المتغيرة / وحدة
و Q = حجم الطلب (كمية الإنتاج التي تُنتج وتُباع أيضاً).
4ـ رسم هذه المعادلات و إختيار البديل الذي يحقق أقل تكاليف كلية ممكنة لحجم الإنتاج أو الحجم الطلب .
ويفترض هذا الأسلوب ما يلي: وجود تكاليف ثابتة عالية، وإن التكاليف المتغيرة للوحدة تتناسب طردياً (علاقة خطية) مع حجم الإنتاج وان التكاليف المتغيرة ستكون مستقرة في المستقبل، وفيما يلي نقدم مثالاً لتوضيح كيفية تطبيق هذا الأسلوب.
مثال (5-1): إفترض أن أحد المصنّعين قد حدد البدائل التالية لتوفير أحد الأجزاء:
1ـ شراء هذا الجزء من خارج الشركة بسعر 2000 دولار وبدون تحمل أي تكاليف ثابتة.
2ـ تصنيع هذا الجزء بإستخدام مخرطة ذات تحكم رقمي NC بكلفة متغيرة مقدارها 750 دينار (بضمنها المواد) وبتكاليف ثابتة 800000 دولار.
3ـ تصنيع هذا الجزء في ورشة ميكانيكية داخل أحد مصانع الشركة بكلفة مقدارها 150 دولار (بضمنها المواد) وبتكاليف ثابتة 2000000 دولار.
المطلوب /
إجراء تحليل نقطة التعادل بيانية (بالرسم) وتحديد البدائل المتاحة لهذا المنتوج لمستويات طلب مختلفة.
الحل : بإستخدام التكاليف الثابتة والتكاليف المتغيرة نقوم بإعداد معادلات التكاليف الكلية كما يلي :
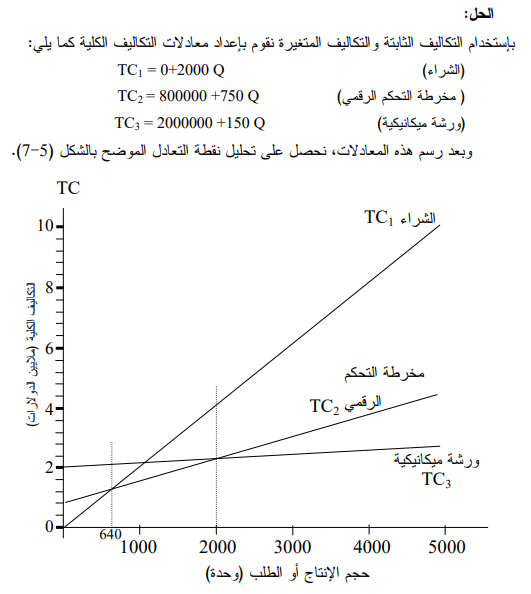
الشكل (7-5) : تحليل نقطة التعادل للمفاضلة بين البدائل لمثال (1-5)
وبدراسة هذا الشكل نستنتج ما يلي :
أـ إذا كان حجم الطلب أقل من 640 وحدة فإن البديل الأول هو المرجح إقتصادياً .
ب ـ إذا كان حجم الإنتاج 640 وحدة بالضبط فأما البديل الأول أو الثاني، وذلك لوجود نقطة تعادل بين البديلين.
ج ـ إذا كان الطلب يقع بين 640 و أقل من 2000 وحدة فإن البديل الثاني هو المرجح اقتصادياً.
د ـ إذا كان حجم الطلب 2000 فأما البديل الثاني أو الثالث وذلك لوجود نقطة تعادل بينهما.
هـ ـ إذا كان حجم الطلب أكثر من 2000 فإن البديل الثالث هو المرجح إقتصادياً.
إن نقطة التقاطع التي تتقاطع فيها خطوط التكاليف الكلية لكل بديل من بدائل نظم العمليات تدعى بنفطة عدم الإهمية أو عدم الإختلاف (Point Of Indifference) وهي النقطة التي تتساوى فيها التكاليف الكلية لبديلين، مما يعني عدم أهمية الفروقات بين البديلين في تلك النقطة التي تمثل حجماً معيناً من الطلب على المنتوج، وإن الفرق بين البديلين يكون مهماً عندما يكون الطلب أعلى أو أدنى من نقطة عدم الأهمية مما يجعل عملية المفاضلة تكتسب أهميتها اقتصادياً.
تحليل نقطة التعادل رياضياً :
يمكن التوصل إلى نتائج عملية المفاضلة بين بدائل نظم العمليات رياضياً بإتباع نفس الخطوات تقريباً عدا الخطوة (2) أدناه :
1 ـ إعداد معادلات الكلفة الكلية لكل بديل وفق المعادلة (4-1) .
2- حساب نقطة أو نقاط عدم الأهمية أو عدم الإختلاف بين كل بديلين من البدائل من خلال مكافأة معادلتي الكلفة الكلية لأي بديلين مراد المفاضلة بينهما، وإيجاد حجم الطلب في نقطة عدم الأهمية الذي تتساوى فيه التكاليف الكلية بين البديلين (المعادلة 5-1 أدناه) .
3 ـ يرجح البديل ذو التكاليف الثابتة الأوطأ عندما يُتوقع أن يسود حجم الطلب أسفل نقطة عدم الإختلاف.
4- يرجح البديل ذو التكاليف المتغيرة الأوطأ عندما يتوقع أن يسود حجم الطلب أعلى أو فوق نقطة عدم الإختلاف أو عدم الأهمية .
5- يعبر عن نقطة الأهمية او عدم الاختلاف بين بديلين بالمعادلة (5-1):
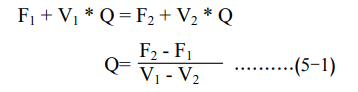
اذ ان :
Q = نقطة عدم الإختلاف بين بديلين (حجم الطلب الذي تتساوى فيه التكاليف الكلية للبديلين).
F1و F2 = التكاليف الثابتة للبديل الأول (1F) و البديل الثاني( F2)
2 V1 V= التكاليف المتغيرة للوحدة البديل الأول (VI) والبديل الثاني (V2).
وبتطبيق بيانات المثال (5-1) نحصل على النتائج الآتية :

وهي نفس النتائج التي تم التوصل لها بالحل البياني ومن ثم تنطبق عليها نفس الاستنتاجات التي ذُكرت آنفاً (ملاحظة : يجب أن تظهر نفس النتائج بالحالتين).
 الاكثر قراءة في نظام الانتاج وانواعه وخصائصه
الاكثر قراءة في نظام الانتاج وانواعه وخصائصه
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


