Confidence Interval

A confidence interval is an interval in which a measurement or trial falls corresponding to a given probability. Usually, the confidence interval of interest is symmetrically placed around the mean, so a 50% confidence interval for a symmetric probability density function would be the interval  such that

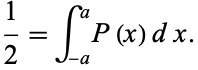(1)

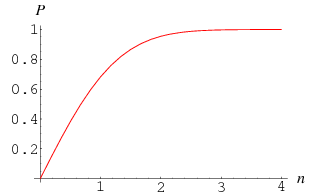
For a normal distribution, the probability that a measurement falls within 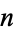 standard deviations (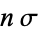) of the mean  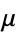(i.e., within the interval ) is given by

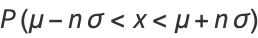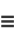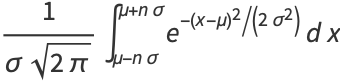			(2)
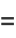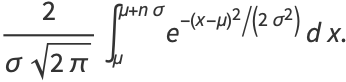			(3)

Now let 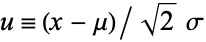, so 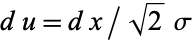. Then

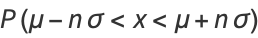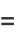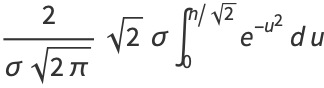			(4)
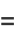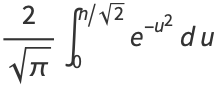			(5)
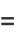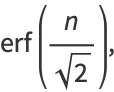			(6)

where 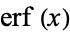 is the so-called erf function. The following table summarizes the probabilities  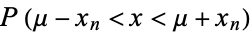that measurements from a normal distribution fall within  for 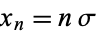 with small values of .

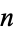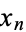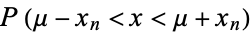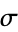	0.6826895
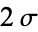	0.9544997
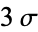	0.9973002
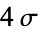	0.9999366
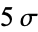	0.9999994

Conversely, to find the probability-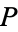 confidence interval centered about the mean for a normal distribution in units of 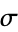, solve equation (5) for  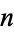to obtain

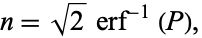(7)

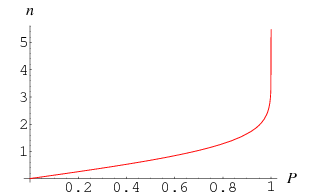
where 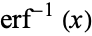 is the inverse erf function. The following table then gives the values of  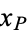such that  is the probability-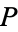 confidence interval for a few representative values of 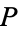. These values can be returned by NormalCI[0, 1, ConfidenceLevel -> P] in the Wolfram Language package HypothesisTesting` .

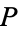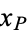0.800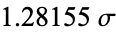
0.900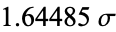
0.950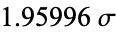
0.990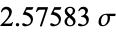
0.995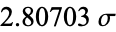
0.999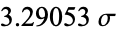

REFERENCES:

Kenney, J. F. and Keeping, E. S. "Confidence Limits for the Binomial Parameter" and "Confidence Interval Charts." §11.4 and 11.5 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 167-169, 1962.