Entropy Form

The last quantity on the right, conditional entropy H_Y|X, as H_X,Y-H_X. Substituting that difference in place of H_Y|X in :
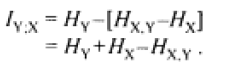(1)
In this form, mutual information is the sum of the two self-entropies minus the joint entropy.

We used the mutually associated case to derive Equation 1. However, Equation 1 also applies to the mutually unassociated case. For that case, mutual information turns out to be zero. To see that, we use the equation for the unassociated case. Using that definition, we substitute H_X+H_Y in place of H_X,Y in Equation 1. That gives I_Y;X=H_Y+H_X- (H_X+H_Y), or I_Y;X=0. So, the mutual information of two independent systems is zero. In other words, one system tells us nothing about the other. Incidentally, rearranging Equation 1 provides an alternate expression for joint entropy, H_X,Y:
H_X,Y = H_Y + H_X-I_Y;X....... (2)
Joint entropy for two systems or dimensions, whether mutually related or not, therefore is the sum of the two self-entropies minus the mutual information. (For two unrelated systems, mutual information I_Y;X is zero. Eq. 2 then reduces, H_X,Y=H_Y+H_X.)

اخر الاخبار

اخبار العتبة العباسية المقدسة

ما الخدمات التي قدّمها موكب أشبال الطفّ لزائري عاشوراء؟

العتبة العباسية المقدسة تنظّم مسيرات عزائية لإحياء ذكرى عاشوراء في نينوى

قسم الشؤون الفكرية يحيي ذكرى استشهاد الإمام الحسين (عليه السلام) في القارة الإفريقية

قسمُ التربية والتعليم يقيم مجلسه العزائي السنوي بذكرى عاشوراء

المزيد

الآخبار الصحية

تناول الجبن.. مفيد للجسم أم خطر يهدد صحتك؟

طبيبة أسنان تحذر.. لا تتجاهل هذه العلامة بعد التنظيف

يجب أن تأكل المزيد من الشمام هذا الصيف.. إليك السبب ؟

تأثير صحي كبير.. كم بيضة يجب أن تتناول يوميا؟

المزيد

الآخبار التكنلوجية

أداء خلايا البيروفسكايت الشمسية تحت الماء قد يزيد كفاءة تحويل الكهرباء

مسافة الأمان: أساس القيادة الآمنة وتجنب الحوادث

هل القيادة السريعة تعني استهلاك اكثر للوقود؟

لماذا يعتبر كوكب المريخ غير صالح للحياة؟

المزيد

مواضيع ذات صلة

جسيمات التماثل الفائق الفوتينوات ، سكواركات ..المادة الظل.. الأكسيونات ..إلخ .

ريادةالانسان للفضاء -قدرة الله في خلق الطيور(كيف الهمت الطيور الانسان )

التجريبية المنطقية وميكانيكا الكم: رؤية كاسيرر بين العلم والفلسفة

المفاهيم الفيزيائية بين الدقة العلمية والتأويل الفلسفي

"توحيد العلوم عبر استبعاد الميتافيزيقا

إرنست ماخ: توحيد الفيزياء عبر الإدراكات الحسية واستبعاد الميتافيزيقا

"الفيزياء بين الكلاسيكية والكم: من حتمية الأشياء إلى نسبية القوانين"

قوانين البقاء في الفيزياء The Conservation Laws of Physics

من كاسيرر إلى ميكانيكا الكم: تطور مفهوم السببية في الفيزياء والفلسفة

نظرة فلسفية لميكانيكا الكم: هل يمكن فهم الحياة بمفاهيم الفيزياء؟

الطول والزمن في النسبية: التحدي الفيزيائي للفلسفة التقليدية

نسبية الطول بين الفيزياء والفلسفة: أينشتاين في مواجهة فالين