


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-3-2021
Date: 17-4-2021
Date: 2-5-2021
|
The expected number of real zeros  of a random polynomial of degree
of a random polynomial of degree  if the coefficients are independent and distributed normally is given by
if the coefficients are independent and distributed normally is given by
 |
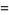 |
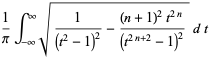 |
(1) |
 |
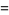 |
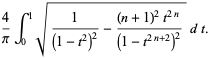 |
(2) |
(Kac 1943, Edelman and Kostlan 1995). Another form of the equation is given by
![E_n=1/piint_(-infty)^inftysqrt([(partial^2)/(partialxpartialy)ln(1-(xy)^(n+1))/(1-xy)]_(x=y=t))dt](https://mathworld.wolfram.com/images/equations/KacFormula/NumberedEquation1.gif) |
(3) |
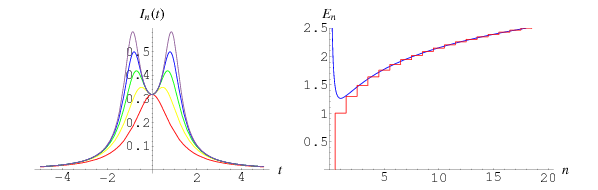
(Kostlan 1993, Edelman and Kostlan 1995). The plots above show the integrand 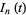 (left) and numerical values of
(left) and numerical values of 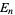 (red curve in right plot) for small
(red curve in right plot) for small 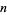 . The first few values are 1, 1.29702, 1.49276, 1.64049, 1.7596, 1.85955, ....
. The first few values are 1, 1.29702, 1.49276, 1.64049, 1.7596, 1.85955, ....
As 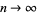 ,
,
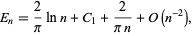 |
(4) |
where
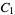 |
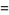 |
![2/pi{ln2+int_0^infty[sqrt(1/(x^2)-(4e^(-2x))/((1-e^(-2x))^2))-1/(x+1)]dx}](https://mathworld.wolfram.com/images/equations/KacFormula/Inline15.gif) |
(5) |
 |
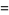 |
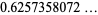 |
(6) |
(OEIS A093601; top curve in right plot above). The initial term was derived by Kac (1943).
REFERENCES:
Edelman, A. and Kostlan, E. "How Many Zeros of a Random Polynomial are Real?" Bull. Amer. Math. Soc. 32, 1-37, 1995.
Kac, M. "On the Average Number of Real Roots of a Random Algebraic Equation." Bull. Amer. Math. Soc. 49, 314-320, 1943.
Kac, M. "A Correction to 'On the Average Number of Real Roots of a Random Algebraic Equation.' " Bull. Amer. Math. Soc. 49, 938, 1943.
Kostan, E. "On the Distribution of Roots in a Random Polynomial." Ch. 38 in From Topology to Computation: Proceedings of the Smalefest (Ed. M. W. Hirsch, J. E. Marsden, and M. Shub). New York: Springer-Verlag, pp. 419-431, 1993.
Sloane, N. J. A. Sequence A093601 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
دراسة تستعرض آلام السجناء السياسيين في حقبة البعث المجرم في العراق
|
|
|