


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-2-2021
Date: 14-2-2016
Date: 27-4-2021
|
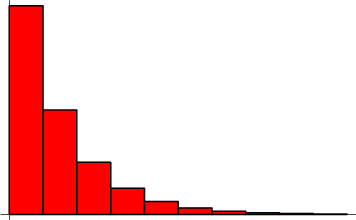
The geometric distribution is a discrete distribution for 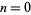 , 1, 2, ... having probability density function
, 1, 2, ... having probability density function
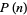 |
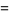 |
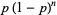 |
(1) |
 |
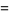 |
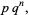 |
(2) |
where 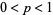 ,
, 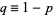 , and distribution function is
, and distribution function is
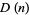 |
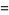 |
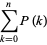 |
(3) |
 |
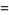 |
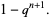 |
(4) |
The geometric distribution is the only discrete memoryless random distribution. It is a discrete analog of the exponential distribution.
Note that some authors (e.g., Beyer 1987, p. 531; Zwillinger 2003, pp. 630-631) prefer to define the distribution instead for 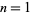 , 2, ..., while the form of the distribution given above is implemented in the Wolfram Language as GeometricDistribution[p].
, 2, ..., while the form of the distribution given above is implemented in the Wolfram Language as GeometricDistribution[p].
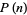 is normalized, since
is normalized, since
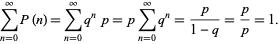 |
(5) |
The raw moments are given analytically in terms of the polylogarithm function,
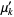 |
 |
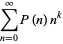 |
(6) |
 |
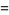 |
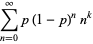 |
(7) |
 |
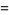 |
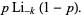 |
(8) |
This gives the first few explicitly as
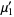 |
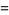 |
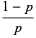 |
(9) |
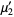 |
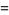 |
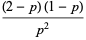 |
(10) |
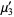 |
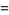 |
![((1-p)[6+(p-6)p])/(p^3)](https://mathworld.wolfram.com/images/equations/GeometricDistribution/Inline35.gif) |
(11) |
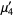 |
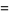 |
![((2-p)(1-p)[12+(p-12)p])/(p^4).](https://mathworld.wolfram.com/images/equations/GeometricDistribution/Inline38.gif) |
(12) |
The central moments are given analytically in terms of the Lerch transcendent as
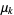 |
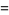 |
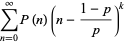 |
(13) |
 |
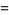 |
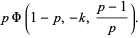 |
(14) |
This gives the first few explicitly as
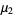 |
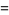 |
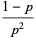 |
(15) |
 |
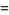 |
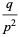 |
(16) |
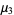 |
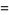 |
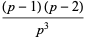 |
(17) |
 |
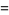 |
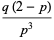 |
(18) |
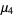 |
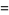 |
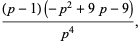 |
(19) |
so the mean, variance, skewness, and kurtosis excess are given by
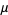 |
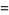 |
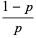 |
(20) |
 |
 |
 |
(21) |
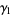 |
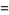 |
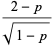 |
(22) |
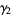 |
 |
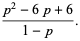 |
(23) |
For the case 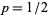 (corresponding to the distribution of the number of coin tosses needed to win in the Saint Petersburg paradox) the formula (23) gives
(corresponding to the distribution of the number of coin tosses needed to win in the Saint Petersburg paradox) the formula (23) gives
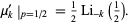 |
(24) |
The first few raw moments are therefore 1, 3, 13, 75, 541, .... Two times these numbers are OEIS A000629, which have exponential generating functions 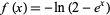 and
and 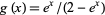 . The mean, variance, skewness, and kurtosis excess of the case
. The mean, variance, skewness, and kurtosis excess of the case 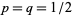 are given by
are given by
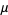 |
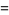 |
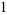 |
(25) |
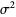 |
 |
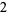 |
(26) |
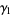 |
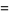 |
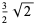 |
(27) |
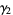 |
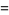 |
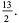 |
(28) |
The characteristic function is given by
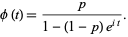 |
(29) |
The first cumulant of the geometric distribution is
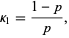 |
(30) |
and subsequent cumulants are given by the recurrence relation
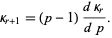 |
(31) |
The mean deviation of the geometric distribution is
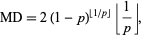 |
(32) |
where 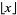 is the floor function.
is the floor function.
REFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 531-532, 1987.
Sloane, N. J. A. Sequence A000629 in "The On-Line Encyclopedia of Integer Sequences."
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 118, 1992.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae, 31st ed. Boca Raton, FL: CRC Press, pp. 630-631, 2003.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|