


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-3-2021
Date: 8-4-2021
Date: 26-4-2021
|
Let 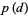 be the probability that a random walk on a
be the probability that a random walk on a 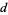 -D lattice returns to the origin. In 1921, Pólya proved that
-D lattice returns to the origin. In 1921, Pólya proved that
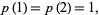 |
(1) |
but
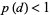 |
(2) |
for 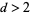 . Watson (1939), McCrea and Whipple (1940), Domb (1954), and Glasser and Zucker (1977) showed that
. Watson (1939), McCrea and Whipple (1940), Domb (1954), and Glasser and Zucker (1977) showed that
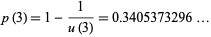 |
(3) |
(OEIS A086230), where
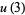 |
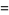 |
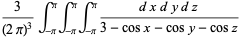 |
(4) |
 |
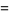 |
![(12)/(pi^2)(18+12sqrt(2)-10sqrt(3)-7sqrt(6)){K[(2-sqrt(3))(sqrt(3)-sqrt(2))]}^2](https://mathworld.wolfram.com/images/equations/PolyasRandomWalkConstants/Inline9.gif) |
(5) |
 |
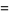 |
![3(18+12sqrt(2)-10sqrt(3)-7sqrt(6))[1+2sum_(k=1)^(infty)exp(-k^2pisqrt(6))]^4](https://mathworld.wolfram.com/images/equations/PolyasRandomWalkConstants/Inline12.gif) |
(6) |
 |
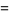 |
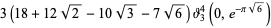 |
(7) |
 |
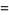 |
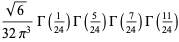 |
(8) |
 |
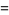 |
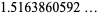 |
(9) |
(OEIS A086231; Borwein and Bailey 2003, Ch. 2, Ex. 20) is the third of Watson's triple integrals modulo a multiplicative constant, 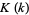 is a complete elliptic integral of the first kind,
is a complete elliptic integral of the first kind, 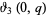 is a Jacobi theta function, and
is a Jacobi theta function, and 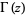 is the gamma function.
is the gamma function.
Closed forms for 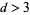 are not known, but Montroll (1956) showed that for
are not known, but Montroll (1956) showed that for 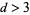 ,
,
![p(d)=1-[u(d)]^(-1),](https://mathworld.wolfram.com/images/equations/PolyasRandomWalkConstants/NumberedEquation4.gif) |
(10) |
where
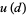 |
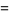 |
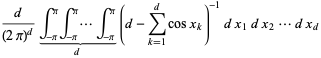 |
(11) |
 |
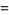 |
![int_0^infty[I_0(t/d)]^de^(-t)dt,](https://mathworld.wolfram.com/images/equations/PolyasRandomWalkConstants/Inline32.gif) |
(12) |
and 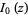 is a modified Bessel function of the first kind.
is a modified Bessel function of the first kind.
Numerical values of 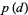 from Montroll (1956) and Flajolet (Finch 2003) are given in the following table.
from Montroll (1956) and Flajolet (Finch 2003) are given in the following table.
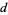 |
OEIS | 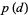 |
| 3 | A086230 | 0.340537 |
| 4 | A086232 | 0.193206 |
| 5 | A086233 | 0.135178 |
| 6 | A086234 | 0.104715 |
| 7 | A086235 | 0.0858449 |
| 8 | A086236 | 0.0729126 |
REFERENCES:
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Finch, S. R. "Pólya's Random Walk Constant." §5.9 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 322-331, 2003.
Domb, C. "On Multiple Returns in the Random-Walk Problem." Proc. Cambridge Philos. Soc. 50, 586-591, 1954.
Glasser, M. L. and Zucker, I. J. "Extended Watson Integrals for the Cubic Lattices." Proc. Nat. Acad. Sci. U.S.A. 74, 1800-1801, 1977.
McCrea, W. H. and Whipple, F. J. W. "Random Paths in Two and Three Dimensions." Proc. Roy. Soc. Edinburgh 60, 281-298, 1940.
Montroll, E. W. "Random Walks in Multidimensional Spaces, Especially on Periodic Lattices." J. SIAM 4, 241-260, 1956.
Sloane, N. J. A. Sequences A086230, A086231, A086232, A086233, A086234, A086235, and A086236 in "The On-Line Encyclopedia of Integer Sequences."
Watson, G. N. "Three Triple Integrals." Quart. J. Math., Oxford Ser. 2 10, 266-276, 1939.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|