ADIABATIC PROCESS

In classical physics, adiabatic processes are mainly associated with thermodynamics and mechanics. In thermodynamics, when changes occur to a system such that it remains in a state of equilibrium with its environment at all the times, such that its entropy remain constant, the process by which such changes occur to a system is called an adiabatic process. For example, consider a gas inside a container that is a thermal insulator. If now the gas expands or contracts without gaining or losing heat energy, then such a process of expansion or contraction of gas is called an adiabatic process. Heat energy and entropy remain constant all the time; thus, heat energy and entropy are called adiabatic invariants.
In mechanical systems, if one of the parameters defining the motion of a system is varied very slowly over a long period of time, the energy is no longer constant in time. However, the action variable for such a system remains constant in time and, thus, is an adiabatic invariant. For example, consider a pendulum whose length “l₀” is reduced to some length “l” very slowly over a long period of time (T ). The action variable of the pendulum which is I = E/ω, (where E is the energy and ω is the angular frequency of the pendulum) remains constant in time. After a very long time, “T,” the energy and angular frequency of oscillations of the pendulum changes, but action variable which is adiabatic invariant remains constant, as shown in Figure 1. The shortening of the string increases the energy and angular frequency of the pendulum.

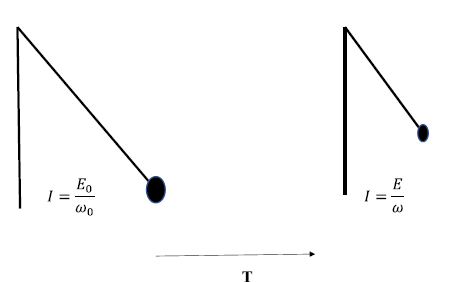
FIGURE 1: An illustration of the adiabatic invariant in a pendulum.

In quantum mechanics, consider a Hamiltonian of a system “H(0)” at time t = 0 which changes very slowly over a very long period of time “T” to H(T ). If initially the system starts out in a stationary state |n(0)〉, what would be the final state of the system after time “T”?
To find an answer to such a question, we need to resort to adiabatic theorem.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

هل هناك حدود للتفسير؟

هل يمكن اختبار نظرية الأوتار تجريبياً؟

ما هو المكان والزمان في الواقع، وهل من الممكن العمل بدونهما؟

آفاق مستقبلية: نظرية الأوتار بين طموح النظرية النهائية وتحديات القرن الحادي والعشرين

هل تؤدي نظرية الأوتار إلى إعادة صياغة ميكانيكا الكم؟

ما هو المبدأ الأساسي في نظرية الأوتار؟

في البدء كانت هناك شذرة لها حجم بلانك(رؤية نظرية الأوتار لبداية الكون)

لماذا ثلاثة؟ تفسير الأبعاد الفضائية الثلاثة في نظرية الأوتار

الكوسمولوجيا ونظرية الأوتار الفائقة

الدخول إلى نظرية الأوتار

ما مدى سواد الأسود؟

أنتروبية الثقوب السوداء