المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Chi Distribution |
 1561
 12:07 صباحاً
date: 3-4-2021 |
Author : Evans, M.; Hastings, N.; and Peacock, B. 
Book or Source : "Chi Distribution." §8.3 in Statistical Distributions, 3rd ed. New York: Wiley 
Page and Part : ...|
Read More
Date: 16-4-2021
1722
Date: 2-5-2021
1652
Date: 22-2-2021
1448
|
The chi distribution with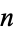 
degrees of freedom is the distribution followed by the square root of a chi-squared random variable. For 
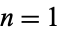, the 
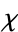distribution is a half-normal distribution with 
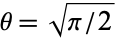. For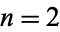 
, it is a Rayleigh distribution with 
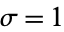. The chi distribution is implemented in the Wolfram Language as ChiDistribution[n].
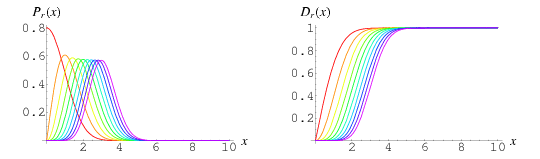
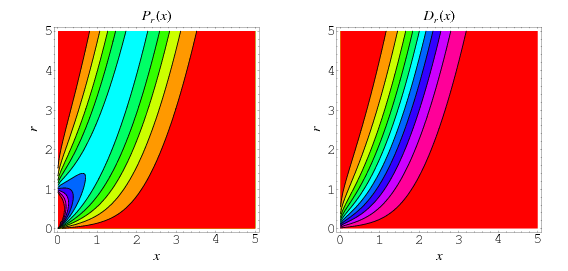
The probability density function and distribution function for this distribution are
 |
 |
 |
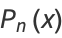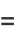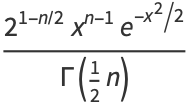(1) |
 |
 |
 |
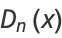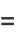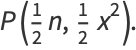(2) |
where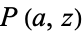 
is a regularized gamma function.
The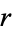 
th raw moment is
 |
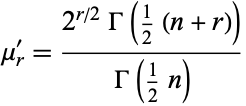(3) |
(Johnson et al. 1994, p. 421; Evans et al. 2000, p. 57; typo corrected), giving the first few as
 |
 |
 |
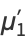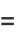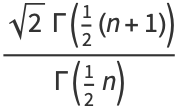(4) |
 |
 |
 |
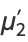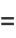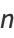(5) |
 |
 |
 |
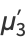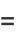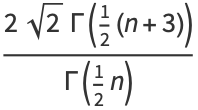(6) |
 |
 |
 |
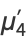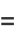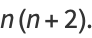(7) |
The mean, variance, skewness, and kurtosis excess are given by
 |
 |
 |
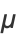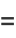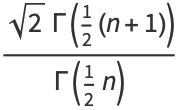(8) |
 |
 |
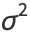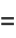![(2[Gamma(1/2n)Gamma(1+1/2n)-Gamma^2(1/2(n+1))])/(Gamma^2(1/2n))](https://mathworld.wolfram.com/images/equations/ChiDistribution/Inline32.gif) |
(9) |
 |
 |
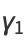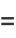![(2Gamma^3(1/2(n+1))-3Gamma(1/2n)Gamma(1/2(n+1))Gamma(1+1/2n))/([Gamma(1/2n)Gamma(1+1/2n)-Gamma^2(1/2(n+1))]^(3/2))+(Gamma^2(1/2n)Gamma((3+n)/2))/([Gamma(1/2n)Gamma(1+1/2n)-Gamma^2(1/2(n+1))]^(3/2))](https://mathworld.wolfram.com/images/equations/ChiDistribution/Inline35.gif) |
(10) |
 |
 |
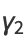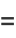![(-3Gamma^4(1/2(n+1))+6Gamma(1/2n)Gamma^2(1/2(n+1))Gamma(1+1/2n))/([Gamma(1/2n)Gamma((2+n)/2)-Gamma^2(1/2(n+1))]^2)+(-4Gamma^2(1/2n)Gamma(1/2(n+1))Gamma((3+n)/2)+Gamma^3(1/2n)Gamma((4+n)/2))/([Gamma(1/2n)Gamma((2+n)/2)-Gamma^2(1/2(n+1))]^2).](https://mathworld.wolfram.com/images/equations/ChiDistribution/Inline38.gif) |
(11) |
REFERENCES:
Evans, M.; Hastings, N.; and Peacock, B. "Chi Distribution." §8.3 in Statistical Distributions, 3rd ed. New York: Wiley, p. 57, 2000.
Johnson, N.; Kotz, S.; and Balakrishnan, N. Continuous Univariate Distributions, Vol. 1, 2nd ed. Boston, MA: Houghton Mifflin, 1994.
|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|
