


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-3-2021
Date: 6-2-2016
Date: 15-3-2021
|

A gamma distribution is a general type of statistical distribution that is related to the beta distribution and arises naturally in processes for which the waiting times between Poisson distributed events are relevant. Gamma distributions have two free parameters, labeled 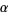 and
and 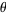 , a few of which are illustrated above.
, a few of which are illustrated above.
Consider the distribution function 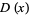 of waiting times until the
of waiting times until the 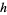 th Poisson event given a Poisson distribution with a rate of change
th Poisson event given a Poisson distribution with a rate of change 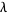 ,
,
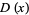 |
 |
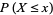 |
(1) |
 |
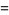 |
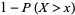 |
(2) |
 |
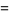 |
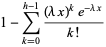 |
(3) |
 |
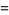 |
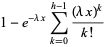 |
(4) |
 |
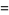 |
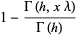 |
(5) |
for 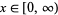 , where
, where 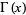 is a complete gamma function, and
is a complete gamma function, and 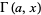 an incomplete gamma function. With
an incomplete gamma function. With 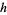 an integer, this distribution is a special case known as the Erlang distribution.
an integer, this distribution is a special case known as the Erlang distribution.
The corresponding probability function 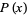 of waiting times until the
of waiting times until the 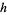 th Poisson event is then obtained by differentiating
th Poisson event is then obtained by differentiating 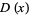 ,
,
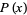 |
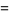 |
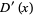 |
(6) |
 |
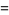 |
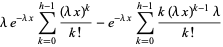 |
(7) |
 |
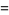 |
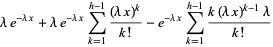 |
(8) |
 |
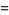 |
![lambdae^(-lambdax)-lambdae^(-lambdax)sum_(k=1)^(h-1)[(k(lambdax)^(k-1))/(k!)-((lambdax)^k)/(k!)]](https://mathworld.wolfram.com/images/equations/GammaDistribution/Inline39.gif) |
(9) |
 |
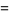 |
![lambdae^(-lambdax){1-sum_(k=1)^(h-1)[((lambdax)^(k-1))/((k-1)!)-((lambdax)^k)/(k!)]}](https://mathworld.wolfram.com/images/equations/GammaDistribution/Inline42.gif) |
(10) |
 |
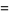 |
![lambdae^(-lambdax){1-[1-((lambdax)^(h-1))/((h-1)!)]}](https://mathworld.wolfram.com/images/equations/GammaDistribution/Inline45.gif) |
(11) |
 |
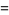 |
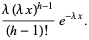 |
(12) |
Now let 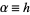 (not necessarily an integer) and define
(not necessarily an integer) and define 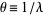 to be the time between changes. Then the above equation can be written
to be the time between changes. Then the above equation can be written
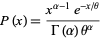 |
(13) |
for 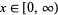 . This is the probability function for the gamma distribution, and the corresponding distribution function is
. This is the probability function for the gamma distribution, and the corresponding distribution function is
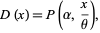 |
(14) |
where 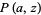 is a regularized gamma function.
is a regularized gamma function.
It is implemented in the Wolfram Language as the function GammaDistribution[alpha, theta].
The characteristic function describing this distribution is
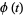 |
 |
![F_x{(x^(-x/theta)x^(alpha-1))/(Gamma(alpha)theta^alpha)[1/2(1+sgnx)]}(t)](https://mathworld.wolfram.com/images/equations/GammaDistribution/Inline55.gif) |
(15) |
 |
 |
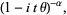 |
(16) |
where ](https://mathworld.wolfram.com/images/equations/GammaDistribution/Inline59.gif) is the Fourier transform with parameters
is the Fourier transform with parameters 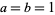 , and the moment-generating function is
, and the moment-generating function is
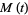 |
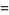 |
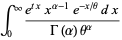 |
(17) |
 |
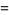 |
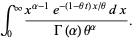 |
(18) |
giving moments about 0 of
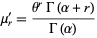 |
(19) |
(Papoulis 1984, p. 147).
In order to explicitly find the moments of the distribution using the moment-generating function, let
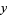 |
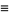 |
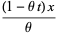 |
(20) |
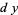 |
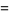 |
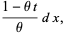 |
(21) |
so
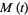 |
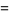 |
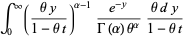 |
(22) |
 |
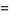 |
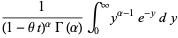 |
(23) |
 |
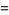 |
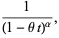 |
(24) |
giving the logarithmic moment-generating function as
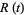 |
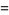 |
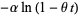 |
(25) |
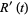 |
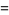 |
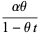 |
(26) |
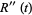 |
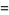 |
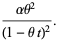 |
(27) |
The mean, variance, skewness, and kurtosis excess are then
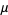 |
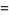 |
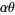 |
(28) |
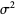 |
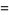 |
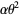 |
(29) |
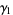 |
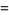 |
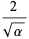 |
(30) |
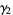 |
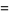 |
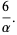 |
(31) |
The gamma distribution is closely related to other statistical distributions. If 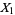 ,
, 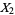 , ...,
, ..., 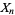 are independent random variates with a gamma distribution having parameters
are independent random variates with a gamma distribution having parameters 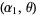 ,
, 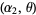 , ...,
, ..., 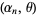 , then
, then 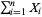 is distributed as gamma with parameters
is distributed as gamma with parameters
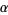 |
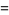 |
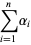 |
(32) |
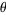 |
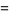 |
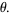 |
(33) |
Also, if 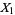 and
and 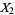 are independent random variates with a gamma distribution having parameters
are independent random variates with a gamma distribution having parameters 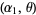 and
and 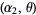 , then
, then 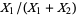 is a beta distribution variate with parameters
is a beta distribution variate with parameters 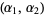 . Both can be derived as follows.
. Both can be derived as follows.
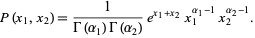 |
(34) |
Let
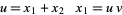 |
(35) |
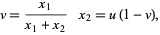 |
(36) |
then the Jacobian is
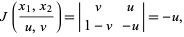 |
(37) |
so
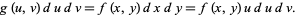 |
(38) |
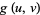 |
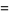 |
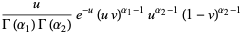 |
(39) |
 |
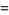 |
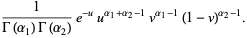 |
(40) |
The sum 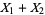 therefore has the distribution
therefore has the distribution
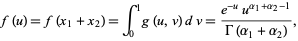 |
(41) |
which is a gamma distribution, and the ratio 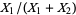 has the distribution
has the distribution
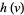 |
 |
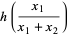 |
(42) |
 |
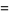 |
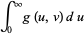 |
(43) |
 |
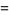 |
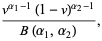 |
(44) |
where 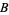 is the beta function, which is a beta distribution.
is the beta function, which is a beta distribution.
If 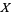 and
and 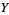 are gamma variates with parameters
are gamma variates with parameters 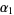 and
and 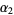 , the
, the 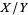 is a variate with a beta prime distribution with parameters
is a variate with a beta prime distribution with parameters 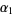 and
and 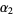 . Let
. Let
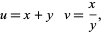 |
(45) |
then the Jacobian is
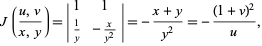 |
(46) |
so
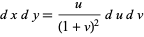 |
(47) |
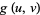 |
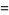 |
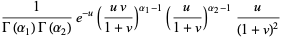 |
(48) |
 |
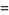 |
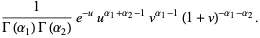 |
(49) |
The ratio 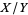 therefore has the distribution
therefore has the distribution
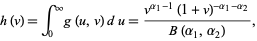 |
(50) |
which is a beta prime distribution with parameters 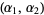 .
.
The "standard form" of the gamma distribution is given by letting 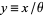 , so
, so 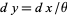 and
and
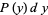 |
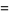 |
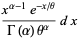 |
(51) |
 |
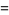 |
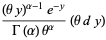 |
(52) |
 |
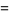 |
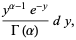 |
(53) |
so the moments about 0 are
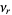 |
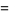 |
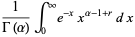 |
(54) |
 |
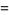 |
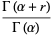 |
(55) |
 |
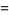 |
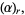 |
(56) |
where 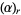 is the Pochhammer symbol. The moments about
is the Pochhammer symbol. The moments about 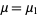 are then
are then
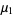 |
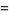 |
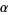 |
(57) |
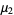 |
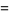 |
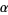 |
(58) |
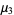 |
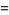 |
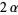 |
(59) |
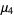 |
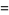 |
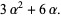 |
(60) |
The moment-generating function is
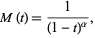 |
(61) |
and the cumulant-generating function is
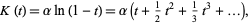 |
(62) |
so the cumulants are
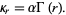 |
(63) |
If 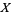 is a normal variate with mean
is a normal variate with mean 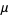 and standard deviation
and standard deviation 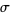 , then
, then
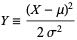 |
(64) |
is a standard gamma variate with parameter 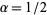 .
.
REFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 534, 1987.
Jambunathan, M. V. "Some Properties of Beta and Gamma Distributions." Ann. Math. Stat. 25, 401-405, 1954.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 103-104, 1984.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|