


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-3-2021
Date: 22-2-2021
Date: 6-2-2016
|
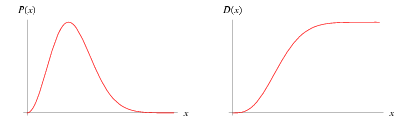
The Maxwell (or Maxwell-Boltzmann) distribution gives the distribution of speeds of molecules in thermal equilibrium as given by statistical mechanics. Defining 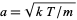 , where
, where 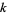 is the Boltzmann constant,
is the Boltzmann constant, 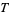 is the temperature,
is the temperature, 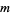 is the mass of a molecule, and letting
is the mass of a molecule, and letting  denote the speed a molecule, the probability and cumulative distributions over the range
denote the speed a molecule, the probability and cumulative distributions over the range 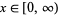 are
are
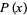 |
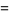 |
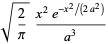 |
(1) |
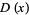 |
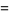 |
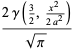 |
(2) |
 |
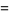 |
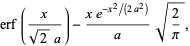 |
(3) |
using the form of Papoulis (1984), where 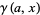 is an incomplete gamma function and
is an incomplete gamma function and 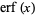 is erf. Spiegel (1992) and von Seggern (1993) each use slightly different definitions of the constant
is erf. Spiegel (1992) and von Seggern (1993) each use slightly different definitions of the constant 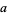 .
.
It is implemented in the Wolfram Language as MaxwellDistribution[sigma].
The 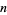 th raw moment is
th raw moment is
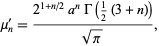 |
(4) |
giving the first few as
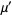 |
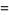 |
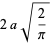 |
(5) |
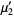 |
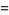 |
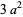 |
(6) |
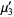 |
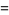 |
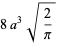 |
(7) |
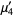 |
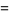 |
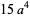 |
(8) |
(Papoulis 1984, p. 149).
The mean, variance, skewness, and kurtosis excess are therefore given by
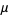 |
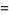 |
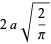 |
(9) |
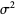 |
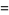 |
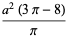 |
(10) |
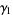 |
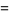 |
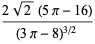 |
(11) |
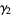 |
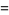 |
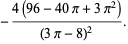 |
(12) |
The characteristic function is
![phi(t)=i{atsqrt(2/pi)-e^(-a^2t^2/2)(a^2t^2-1)×[sgn(t)erfi((a|t|)/(sqrt(2)))-i]},](https://mathworld.wolfram.com/images/equations/MaxwellDistribution/NumberedEquation2.gif) |
(13) |
where 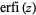 is the erfi function.
is the erfi function.
REFERENCES:
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 104 and 148-149, 1984.
Spiegel, M. R. Schaum's Outline of Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 119, 1992.
von Seggern, D. CRC Standard Curves and Surfaces. Boca Raton, FL: CRC Press, p. 252, 1993.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|