
Rényi,s Parking Constants
 المؤلف:
Mannion, D.
المؤلف:
Mannion, D.
 المصدر:
"Random Space-Filling in One Dimension." Publ. Math. Inst. Hung. Acad. Sci. 9
المصدر:
"Random Space-Filling in One Dimension." Publ. Math. Inst. Hung. Acad. Sci. 9
 الجزء والصفحة:
...
الجزء والصفحة:
...
 20-4-2021
20-4-2021
 3840
3840
Rényi's Parking Constants
Given the closed interval ![[0,x]](https://mathworld.wolfram.com/images/equations/RenyisParkingConstants/Inline1.gif) with
with 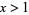 , let one-dimensional "cars" of unit length be parked randomly on the interval. The mean number
, let one-dimensional "cars" of unit length be parked randomly on the interval. The mean number 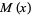 of cars which can fit (without overlapping!) satisfies
of cars which can fit (without overlapping!) satisfies
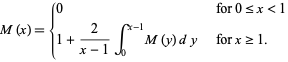 |
(1)
|
The mean density of the cars for large  is
is
(OEIS A050996). While the inner integral can be done analytically,
where 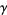 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 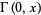 is the incomplete gamma function, it is not known how to do the outer one
is the incomplete gamma function, it is not known how to do the outer one
where 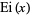 is the exponential integral. The slowly converging series expansion for the integrand is given by
is the exponential integral. The slowly converging series expansion for the integrand is given by
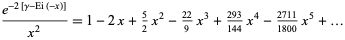 |
(10)
|
(OEIS A050994 and A050995).
In addition,
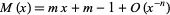 |
(11)
|
for all 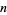 (Rényi 1958), which was strengthened by Dvoretzky and Robbins (1964) to
(Rényi 1958), which was strengthened by Dvoretzky and Robbins (1964) to
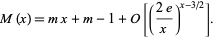 |
(12)
|
Dvoretzky and Robbins (1964) also proved that
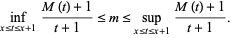 |
(13)
|
Let 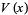 be the variance of the number of cars, then Dvoretzky and Robbins (1964) and Mannion (1964) showed that
be the variance of the number of cars, then Dvoretzky and Robbins (1964) and Mannion (1964) showed that
(OEIS A086245), where
and the numerical value is due to Blaisdell and Solomon (1970). Dvoretzky and Robbins (1964) also proved that
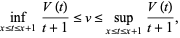 |
(19)
|
and that
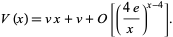 |
(20)
|
Palasti (1960) conjectured that in two dimensions,
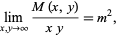 |
(21)
|
but this has not yet been proven or disproven (Finch 2003).
REFERENCES:
Blaisdell, B. E. and Solomon, H. "On Random Sequential Packing in the Plane and a Conjecture of Palasti." J. Appl. Prob. 7, 667-698, 1970.
Dvoretzky, A. and Robbins, H. "On the Parking Problem." Publ. Math. Inst. Hung. Acad. Sci. 9, 209-224, 1964.
Finch, S. R. "Rényi's Parking Constant." §5.3 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 278-284, 2003.
Mannion, D. "Random Space-Filling in One Dimension." Publ. Math. Inst. Hung. Acad. Sci. 9, 143-154, 1964.
Palasti, I. "On Some Random Space Filling Problems." Publ. Math. Inst. Hung. Acad. Sci. 5, 353-359, 1960.
Rényi, A. "On a One-Dimensional Problem Concerning Random Space-Filling." Publ. Math. Inst. Hung. Acad. Sci. 3, 109-127, 1958.
Sloane, N. J. A. Sequences A050994, A050995, A050996, and A086245 in "The On-Line Encyclopedia of Integer Sequences."
Solomon, H. and Weiner, H. J. "A Review of the Packing Problem." Comm. Statist. Th. Meth. 15, 2571-2607, 1986.
 الاكثر قراءة في الاحتمالات و الاحصاء
الاكثر قراءة في الاحتمالات و الاحصاء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


