


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-8-2021
Date: 30-5-2021
Date: 15-7-2021
|
A branch of mathematics which brings together ideas from algebraic geometry, linear algebra, and number theory. In general, there are two main types of 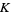 -theory: topological and algebraic.
-theory: topological and algebraic.
Topological 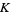 -theory is the "true"
-theory is the "true" 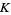 -theory in the sense that it came first. Topological
-theory in the sense that it came first. Topological 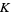 -theory has to do with vector bundles over topological spaces. Elements of a
-theory has to do with vector bundles over topological spaces. Elements of a 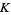 -theory are stable equivalence classes of vector bundles over a topological space. You can put a ring structure on the collection of stably equivalent bundles by defining addition through the Whitney sum, and multiplication through the tensor product of vector bundles. This defines "the reduced real topological
-theory are stable equivalence classes of vector bundles over a topological space. You can put a ring structure on the collection of stably equivalent bundles by defining addition through the Whitney sum, and multiplication through the tensor product of vector bundles. This defines "the reduced real topological 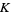 -theory of a space."
-theory of a space."
"The reduced 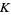 -theory of a space" refers to the same construction, but instead of real vector bundles, complex vector bundles are used. Topological
-theory of a space" refers to the same construction, but instead of real vector bundles, complex vector bundles are used. Topological 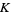 -theory is significant because it forms a generalized cohomology theory, and it leads to a solution to the vector fields on spheres problem, as well as to an understanding of the
-theory is significant because it forms a generalized cohomology theory, and it leads to a solution to the vector fields on spheres problem, as well as to an understanding of the 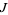 -homeomorphism of homotopy theory.
-homeomorphism of homotopy theory.
Algebraic 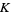 -theory is somewhat more involved. Swan (1962) noticed that there is a correspondence between the category of suitably nice topological spaces (something like regular T2-spaces) and C-*-algebras. The idea is to associate to every space the C-*-algebra of continuous maps from that space to the reals.
-theory is somewhat more involved. Swan (1962) noticed that there is a correspondence between the category of suitably nice topological spaces (something like regular T2-spaces) and C-*-algebras. The idea is to associate to every space the C-*-algebra of continuous maps from that space to the reals.
A vector bundle over a space has sections, and these sections can be multiplied by continuous functions to the reals. Under Swan's correspondence, vector bundles correspond to modules over the C-*-algebra of continuous functions, the modules being the modules of sections of the vector bundle. This study of modules over C-*-algebra is the starting point of algebraic 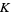 -theory.
-theory.
The Quillen-Lichtenbaum conjecture connects algebraic 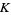 -theory to Étale cohomology.
-theory to Étale cohomology.
REFERENCES:
Atiyah, M. F. K-Theory. New York: Benjamin, 1967.
Bass, H.; Kuku, A. O.; and Pedrini, C. Proceedings of the Workshop and Symposium: Algebraic K-Theory and Its Applications, ICTP, Trieste, Italy, 1-19 Sept. 1997. Singapore: World Scientific, 1999.
Raskind, W. and Weibel, C. (Eds.). Algebraic K-Theory: AMS-IMS-SIAM Joint Summer Research Conference on Algebraic K-Theory, July 13-24, 1997, University of Washington, Seattle. Providence, RI: Amer. Math. Soc., 1997.
Srinivas, V. Algebraic K-Theory, 2nd ed. Boston, MA: Birkhäuser, 1995.
Swan, R. G. "Vector Bundles and Projective Modules." Trans. Amer. Math. Soc. 105, 264-277, 1962.



|
|
|
|
هل تعرف كيف يؤثر الطقس على ضغط إطارات سيارتك؟ إليك الإجابة
|
|
|
|
|
|
|
معهد القرآن الكريم النسوي يقدم خدماته لزائري الإمام الكاظم (عليه السلام)
|
|
|