


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-8-2021
Date: 5-7-2021
Date: 21-6-2017
|
Color each segment of a knot diagram using one of three colors. If
1. At any crossing, either the colors are all different or all the same, and
2. At least two colors are used,
then a knot is said to be three-colorable (or sometimes, simply "colorable"). Colorability is invariant under Reidemeister moves, and can be generalized. For instance, for five colors 0, 1, 2, 3, and 4, a knot is five-colorable if
1. At any crossing, three segments meet. If the overpass is numbered 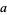 and the two underpasses
and the two underpasses 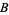 and
and 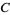 , then
, then 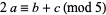 , and
, and
2. At least two colors are used.
Colorability cannot always distinguish handedness. For instance, three-colorability can distinguish the mirror images of the trefoil knot but not the figure eight knot. Five-colorability, on the other hand, distinguishes the mirror images of the figure eight knot but not the trefoil knot.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|