


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-6-2021
Date: 21-7-2021
Date: 26-5-2021
|
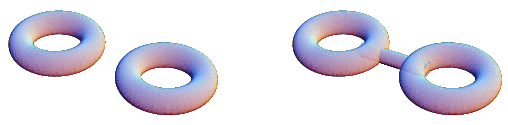
Two oriented knots (or links) can be summed by placing them side by side and joining them by straight bars so that orientation is preserved in the sum. The knot sum is also known as composition (Adams 1994) or connected sum (Rolfsen 1976, p. 40).
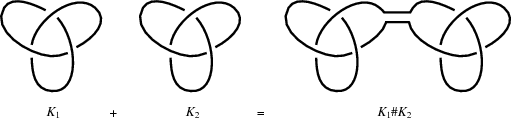
This operation is denoted #, so the knot sum of knots 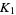 and
and 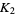 is written
is written
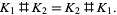 |
The figure above illustrated the knot sum of two trefoil knots having the same handedness.
The knot sum is in general not a well-defined operation, but depends on the choice of balls where the connection is made and perhaps also on the choice of the attaching homeomorphism. The square knot and granny knot illustrate this ambiguity (Rolfsen 1976, pp. 40-41).
Schubert (1949) showed that every knot can be uniquely decomposed (up to the order in which the decomposition is performed) as a knot sum of a class of knots known as prime knots, which cannot themselves be further decomposed. Knots that are the sums of prime knots are known as composite knots.
The knot sum of any knot 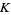 with the unknot is again
with the unknot is again 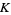 (Adams 1994, p. 8). The knot sum of any number of knots cannot be the unknot unless each knot in the sum is the unknot (Schubert 1949; Steinhaus 1999, p. 265).
(Adams 1994, p. 8). The knot sum of any number of knots cannot be the unknot unless each knot in the sum is the unknot (Schubert 1949; Steinhaus 1999, p. 265).
REFERENCES:
Adams, C. C. "Composition of Knots." §1.2 in The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 7-12, 1994.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 206-207, 1976.
Schubert, H. Sitzungsber. Heidelberger Akad. Wiss., Math.-Naturwiss. Klasse, 3rd Abhandlung. 1949.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, 1999.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|