


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-6-2021
Date: 26-5-2021
Date: 23-7-2021
|
Let 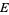 be a compact connected subset of
be a compact connected subset of 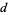 -dimensional Euclidean space. Gross (1964) and Stadje (1981) proved that there is a unique real number
-dimensional Euclidean space. Gross (1964) and Stadje (1981) proved that there is a unique real number 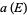 such that for all
such that for all 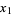 ,
, 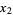 , ...,
, ..., 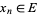 , there exists
, there exists 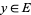 with
with
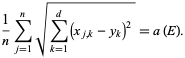 |
(1) |
The magic constant 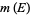 of
of 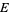 is defined by
is defined by
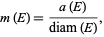 |
(2) |
where
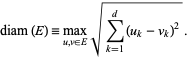 |
(3) |
These numbers are also called dispersion numbers and rendezvous values. For any 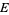 , Gross (1964) and Stadje (1981) proved that
, Gross (1964) and Stadje (1981) proved that
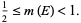 |
(4) |
If 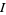 is a subinterval of the line and
is a subinterval of the line and 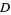 is a circular disk in the plane, then
is a circular disk in the plane, then
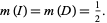 |
(5) |
If 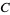 is a circle, then
is a circle, then
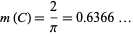 |
(6) |
(OEIS A060294). An expression for the magic constant of an ellipse in terms of its semimajor and semiminor axes lengths is not known. Nikolas and Yost (1988) showed that for a Reuleaux triangle 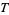
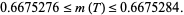 |
(7) |
Denote the maximum value of 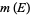 in
in 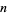 -dimensional space by
-dimensional space by 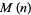 . Then
. Then
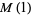 |
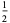 |
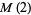 |
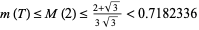 |
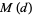 |
![d/(d+1)<=M(d)<=([Gamma(1/2d)]^22^(d-2)sqrt(2d))/(Gamma(d-1/2)sqrt((d+1)pi))<sqrt(d/(d+1))](https://mathworld.wolfram.com/images/equations/MagicGeometricConstants/Inline23.gif) |
where 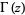 is the gamma function (Nikolas and Yost 1988).
is the gamma function (Nikolas and Yost 1988).
An unrelated quantity characteristic of a given magic square is also known as a magic constant.
REFERENCES:
Finch, S. R. "Rendezvous Constants." §8.21 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 537-542, 2003.
Cleary, J.; Morris, S. A.; and Yost, D. "Numerical Geometry--Numbers for Shapes." Amer. Math. Monthly 95, 260-275, 1986.
Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, 1994.
Gross, O. The Rendezvous Value of Metric Space. Princeton, NJ: Princeton University Press, pp. 49-53, 1964.
Nikolas, P. and Yost, D. "The Average Distance Property for Subsets of Euclidean Space." Arch. Math. (Basel) 50, 380-384, 1988.
Sloane, N. J. A. Sequence A060294 in "The On-Line Encyclopedia of Integer Sequences."
Stadje, W. "A Property of Compact Connected Spaces." Arch. Math. (Basel) 36, 275-280, 1981.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تحتفي بذكرى ولادة الإمام الجواد (عليه السلام) في مشاتل الكفيل
|
|
|