المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | One-Point Compactification |
 1156
 06:24 مساءً
date: 24-7-2021 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : www.almerja.com 
Page and Part : ...|
Read More
Date: 11-7-2021
1624
Date: 15-6-2021
3620
Date: 13-7-2021
2137
|
A topological space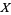 
has a one-point compactification if and only if it is locally compact.
To see a part of this, assume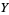 
is compact, 
, 
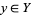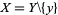and 
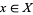. Let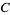 
be a compact neighborhood of 
(relative to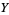 
), not containing 
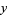. Then 
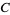is also compact relative to 
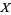, which shows 
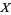is locally compact.
The point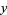 
is often called the point of infinity.
A one-point compactification opens up for simplifications in definitions and proofs.
The continuous functions on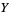 
may be of importance. Their restriction to 
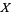are loosely the continuous functions on 
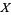with a limit at infinity.
|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|
