


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-5-2021
Date: 23-5-2021
Date: 26-5-2021
|

Let 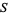 be a subset of a metric space. Then the set
be a subset of a metric space. Then the set 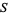 is open if every point in
is open if every point in 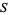 has a neighborhood lying in the set. An open set of radius
has a neighborhood lying in the set. An open set of radius 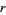 and center
and center 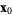 is the set of all points
is the set of all points  such that
such that 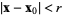 , and is denoted
, and is denoted 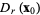 . In one-space, the open set is an open interval. In two-space, the open set is a disk. In three-space, the open set is a ball.
. In one-space, the open set is an open interval. In two-space, the open set is a disk. In three-space, the open set is a ball.
More generally, given a topology (consisting of a set 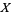 and a collection of subsets
and a collection of subsets 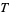 ), a set is said to be open if it is in
), a set is said to be open if it is in 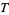 . Therefore, while it is not possible for a set to be both finite and open in the topology of the real line (a single point is a closed set), it is possible for a more general topological set to be both finite and open.
. Therefore, while it is not possible for a set to be both finite and open in the topology of the real line (a single point is a closed set), it is possible for a more general topological set to be both finite and open.
The complement of an open set is a closed set. It is possible for a set to be neither open nor closed, e.g., the half-closed interval ![(0,1]](https://mathworld.wolfram.com/images/equations/OpenSet/Inline12.gif) .
.
REFERENCES:
Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 2, 1991.
Krantz, S. G. Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 3, 1999.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
في مدينة الهرمل اللبنانية.. وفد العتبة الحسينية المقدسة يستمر بإغاثة العوائل السورية المنكوبة
|
|
|