المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Cobweb Equation |
 1849
 01:55 صباحاً
date: 18-8-2021 |
Author : Ezekiel, M 
Book or Source : "The Cobweb Theorem." Quart. J. Econ. 5 
Page and Part : ...|
Read More
Date: 28-9-2021
648
Date: 10-11-2021
743
Date: 21-12-2021
1429
|
The simple first-order difference equation
 |
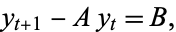(1) |
where
 |
 |
 |
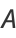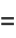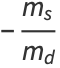(2) |
 |
 |
 |
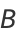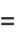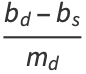(3) |
and
 |
 |
 |
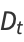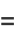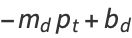(4) |
 |
 |
 |
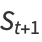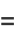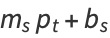(5) |
are the price-demand and price-supply curves, where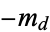 
and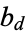 
represent the slope and 
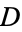-intercept, respectively, for the demand curve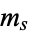, and 
and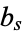 
represent the corresponding constants for the supply curve (Ezekiel 1938, Goldberg 1986).
A class of behaviors related to this equation is known as "Cobweb phenomena" in economics.
REFERENCES:
Ezekiel, M. "The Cobweb Theorem." Quart. J. Econ. 52, 255-280, 1938.
Goldberg, S. Introduction to Difference Equations, with Illustrative Examples from Economics, Psychology, and Sociology. New York: Dover, 1986.
|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|
