


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-8-2021
Date: 30-11-2021
Date: 17-10-2021
|

The Haferman carpet is the beautiful fractal constructed using string rewriting beginning with a cell [1] and iterating the rules
![{0->[1 1 1; 1 1 1; 1 1 1],1->[0 1 0; 1 0 1; 0 1 0]}](https://mathworld.wolfram.com/images/equations/HafermanCarpet/NumberedEquation1.gif) |
(1) |
(Allouche and Shallit 2003, p. 407).

Taking five iterations gives the beautiful pattern illustrated above.

This fractal also appears on the cover of Allouche and Shallit (2003).
Let 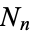 be the number of black boxes,
be the number of black boxes, 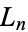 the length of a side of a white box, and
the length of a side of a white box, and 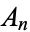 the fractional area of black boxes after the
the fractional area of black boxes after the 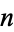 th iteration. Then
th iteration. Then
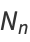 |
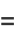 |
![1/(14)[(-1)^n5^(n+1)+9^(n+1)]](https://mathworld.wolfram.com/images/equations/HafermanCarpet/Inline7.gif) |
(2) |
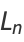 |
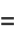 |
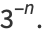 |
(3) |
The numbers of black cells after 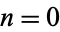 , 1, 2, ... iterations are therefore 1, 4, 61, 424, 4441, 36844, ... (OEIS A118005). The capacity dimension is therefore
, 1, 2, ... iterations are therefore 1, 4, 61, 424, 4441, 36844, ... (OEIS A118005). The capacity dimension is therefore
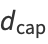 |
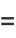 |
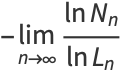 |
(4) |
 |
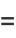 |
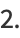 |
(5) |
REFERENCES:
Allouche, J.-P. and Shallit, J. Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, 2003.
Sloane, N. J. A. Sequence A118005 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|