


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-9-2021
Date: 30-11-2021
Date: 14-9-2021
|
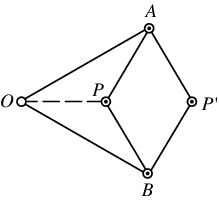
A linkage with six rods which draws the inverse of a given curve. When a pencil is placed at 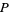 , the inverse is drawn at
, the inverse is drawn at 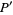 (or vice versa). If a seventh rod (dashed) is added (with an additional pivot),
(or vice versa). If a seventh rod (dashed) is added (with an additional pivot),  is kept on a circle and the locus traced out by
is kept on a circle and the locus traced out by 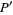 is a straight line. It therefore converts circular motion to linear motion without sliding, and was discovered in 1864. Another linkage which performs this feat using hinged squares had been published by Sarrus in 1853 but ignored. Coxeter (1969, p. 428) shows that
is a straight line. It therefore converts circular motion to linear motion without sliding, and was discovered in 1864. Another linkage which performs this feat using hinged squares had been published by Sarrus in 1853 but ignored. Coxeter (1969, p. 428) shows that
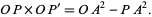 |
REFERENCES:
Bogomolny, A. "Peaucellier Linkage." http://www.cut-the-knot.org/pythagoras/invert.shtml.
Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods. Oxford, England: Oxford University Press, p. 156, 1978.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, pp. 82-83, 1969.
Durell, C. V. Modern Geometry: The Straight Line and Circle. London: Macmillan, p. 117, 1928.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 46-48, 1990.
Rademacher, H. and Toeplitz, O. The Enjoyment of Mathematics: Selections from Mathematics for the Amateur. Princeton, NJ: Princeton University Press, pp. 121-126, 1957.
Sarrus. Comptes Rendus de l'Académie de Paris 36, 1036, 1853.
Smith, D. E. A Source Book in Mathematics. New York: Dover, p. 324, 1994.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, p. 139, 1999.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 120 and 181-182, 1991.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|