


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-12-2021
Date: 10-12-2021
Date: 12-12-2021
|
Laguerre-Gauss quadrature, also called Gauss-Laguerre quadrature or Laguerre quadrature, is a Gaussian quadrature over the interval 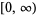 with weighting function
with weighting function 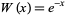 (Abramowitz and Stegun 1972, p. 890). It fits all polynomials of degree
(Abramowitz and Stegun 1972, p. 890). It fits all polynomials of degree 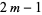 exactly (Chandrasekhar 1960, p. 61).
exactly (Chandrasekhar 1960, p. 61).
The abscissas for quadrature order 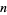 are given by the roots of the Laguerre polynomials
are given by the roots of the Laguerre polynomials 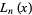 . The weights are
. The weights are
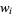 |
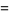 |
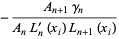 |
(1) |
 |
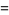 |
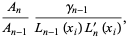 |
(2) |
where 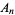 is the coefficient of
is the coefficient of 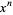 in
in 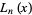 . For Laguerre polynomials,
. For Laguerre polynomials,
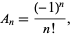 |
(3) |
where 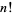 is a factorial, so
is a factorial, so
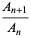 |
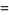 |
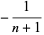 |
(4) |
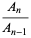 |
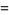 |
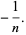 |
(5) |
Additionally,
![gamma_n=int_0^inftyW(x)[L_n(x)]^2dx=1,](https://mathworld.wolfram.com/images/equations/Laguerre-GaussQuadrature/NumberedEquation2.gif) |
(6) |
so
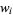 |
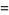 |
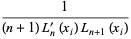 |
(7) |
 |
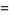 |
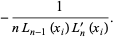 |
(8) |
Using the recurrence relation
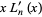 |
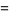 |
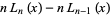 |
(9) |
 |
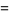 |
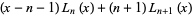 |
(10) |
which, since 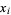 is a root of
is a root of 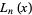 , gives
, gives
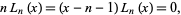 |
(11) |
so (10) becomes
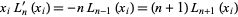 |
(12) |
gives
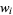 |
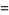 |
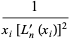 |
(13) |
 |
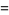 |
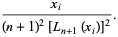 |
(14) |
The error term is
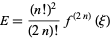 |
(15) |
(Abramowitz and Stegun 1972, p. 890).
Beyer (1987) gives a table of abscissas and weights up to 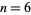 .
.
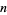 |
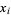 |
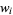 |
| 2 | 0.585786 | 0.853553 |
| 3.41421 | 0.146447 | |
| 3 | 0.415775 | 0.711093 |
| 2.29428 | 0.278518 | |
| 6.28995 | 0.0103893 | |
| 4 | 0.322548 | 0.603154 |
| 1.74576 | 0.357419 | |
| 4.53662 | 0.0388879 | |
| 9.39507 | 0.000539295 | |
| 5 | 0.26356 | 0.521756 |
| 1.4134 | 0.398667 | |
| 3.59643 | 0.0759424 | |
| 7.08581 | 0.00361176 | |
| 12.6408 | 0.00002337 |
The abscissas and weights can be computed analytically for small 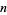 .
.
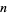 |
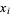 |
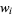 |
| 2 | 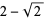 |
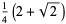 |
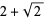 |
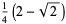 |
For the generalized Laguerre polynomial 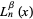 with weighting function
with weighting function 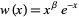 ,
,
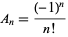 |
(16) |
is the coefficient of 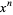 in
in 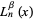 and
and
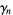 |
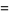 |
![int_0^inftyx^betae^(-x)[L_n^beta(x)]^2dx](https://mathworld.wolfram.com/images/equations/Laguerre-GaussQuadrature/Inline60.gif) |
(17) |
 |
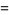 |
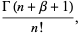 |
(18) |
where 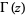 is the gamma function. The weights are then
is the gamma function. The weights are then
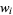 |
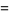 |
![(Gamma(n+beta)x_i)/(n!(n+beta)[L_(n-1)^beta(x_i)]^2)](https://mathworld.wolfram.com/images/equations/Laguerre-GaussQuadrature/Inline67.gif) |
(19) |
 |
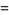 |
![(Gamma(n+beta+1)x_i)/(n!(n+1)^2[L_(n+1)^beta(x_i)]^2),](https://mathworld.wolfram.com/images/equations/Laguerre-GaussQuadrature/Inline70.gif) |
(20) |
and the error term is
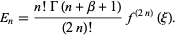 |
(21) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 890 and 923, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 463, 1987.
Chandrasekhar, S. Radiative Transfer. New York: Dover, pp. 61 and 64-65, 1960.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 325-327, 1956.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
قسم الشؤون الفكرية يصدر كتاب الفلسفة الغربية برؤية الشيخ مرتضى مطهري
|
|
|