Halley's Method

A root-finding algorithm also known as the tangent hyperbolas method or Halley's rational formula. As in Halley's irrational formula, take the second-order Taylor series

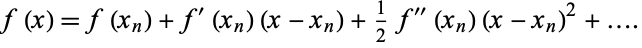(1)

A root of 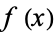 satisfies 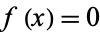, so

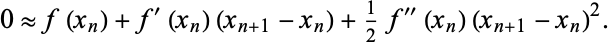(2)

Now write

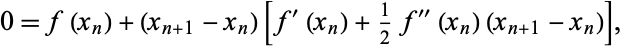(3)

giving

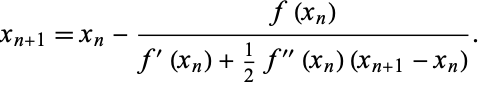(4)

Using the result from Newton's method,

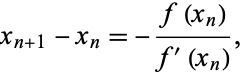(5)

gives

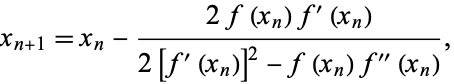(6)

so the iteration function is

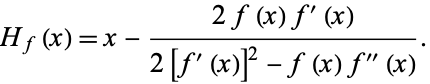(7)

This satisfies 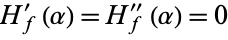 where 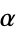 is a root, so it is third order for simple zeros. Curiously, the third derivative

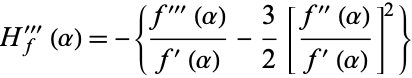(8)

is the Schwarzian derivative. Halley's method may also be derived by applying Newton's method to 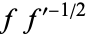. It may also be derived by using an osculating curve of the form

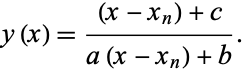(9)

Taking derivatives,

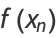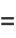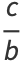			(10)
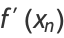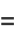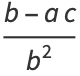			(11)
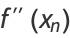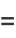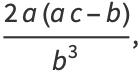			(12)

which has solutions

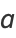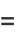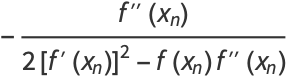			(13)
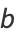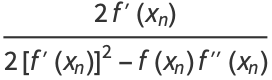			(14)
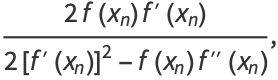			(15)

so at a root, 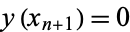 and

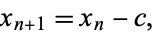(16)

which is Halley's method.

REFERENCES:

Ortega, J. M. and Rheinboldt, W. C. Iterative Solution of Nonlinear Equations in Several Variables. Philadelphia, PA: SIAM, 2000.

Scavo, T. R. and Thoo, J. B. "On the Geometry of Halley's Method." Amer. Math. Monthly 102, 417-426, 1995.