


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-8-2021
Date: 16-10-2021
Date: 11-9-2021
|
There are two sorts of transforms known as the fractional Fourier transform.
The linear fractional Fourier transform is a discrete Fourier transform in which the exponent is modified by the addition of a factor 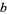 ,
,
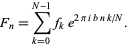 |
However, such transforms may not be consistent with their inverses unless 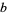 is an integer relatively prime to
is an integer relatively prime to 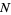 so that
so that 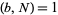 . Fractional fourier transforms are implemented in the Wolfram Language as Fourier[list, FourierParameters ->
. Fractional fourier transforms are implemented in the Wolfram Language as Fourier[list, FourierParameters -> 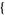 a, b
a, b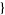 ], where
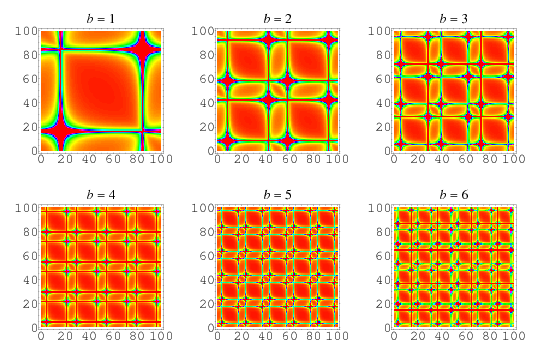
], where 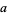 is an additional scaling parameter. For example, the plots above show 2-dimensional fractional Fourier transforms of the function
is an additional scaling parameter. For example, the plots above show 2-dimensional fractional Fourier transforms of the function 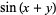 for parameter
for parameter 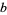 ranging from 1 to 6.
ranging from 1 to 6.
The quadratic fractional Fourier transform is defined in signal processing and optics. Here, the fractional powers 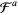 of the ordinary Fourier transform operation
of the ordinary Fourier transform operation 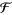 correspond to rotation by angles
correspond to rotation by angles 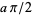 in the time-frequency or space-frequency plane (phase space). So-called fractional Fourier domains correspond to oblique axes in the time-frequency plane, and thus the fractional Fourier transform (sometimes abbreviated FRT) is directly related to the Radon transforms of the Wigner distribution and the ambiguity function. Of particular interest from a signal processing perspective is the concept of filtering in fractional Fourier domains. Physically, the transform is intimately related to Fresnel diffraction in wave and beam propagation and to the quantum-mechanical harmonic oscillator.
in the time-frequency or space-frequency plane (phase space). So-called fractional Fourier domains correspond to oblique axes in the time-frequency plane, and thus the fractional Fourier transform (sometimes abbreviated FRT) is directly related to the Radon transforms of the Wigner distribution and the ambiguity function. Of particular interest from a signal processing perspective is the concept of filtering in fractional Fourier domains. Physically, the transform is intimately related to Fresnel diffraction in wave and beam propagation and to the quantum-mechanical harmonic oscillator.
REFERENCES:
Ozaktas, H. M.; Zalevsky, Z.; and Kutay, M. A. The Fractional Fourier Transform, with Applications in Optics and Signal Processing. New York: Wiley, 2000. http://www.ee.bilkent.edu.tr/~haldun/wileybook.html.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|