


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 19-11-2020
التاريخ: 19-1-2022
التاريخ: 23-1-2022
التاريخ: 19-1-2022
|
طريقة المربعات الصغرى Least Square Method
تستخدم هذه الطريقة لرسم أفضل خط مستقيم يمر بمجموعة من النقاط (أو بعضها). لنفترض أن لدينا مجموعة من البيانات تمثل بعائلة من النقاط (كل منها لها إحداثيان y, x). أي أن هذه النقاط هي:
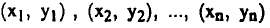
ونريد الآن رسم خط مستقيم يمر بكل أو بمعظم هذه النقاط .
تعطي معادلة الخط المستقيم بالعلاقة:
y = mx+c
حيث m ميل الخط.
C طول الجزء المقطوع من محور الصادات (y) .
لاحظ أنه لكل قيمة من قيم x المقاسة (box) توجد قيمتان للمتغير لا. أحدهما هي قيمة y المقاسة (yob) والأخرى هي قيمة لا الواقعة على الخط المستقيم. وقد تختلف هاتان القيمتان عن بعضهما ونعبر عن الاختلاف بالرمز ى حيث.
(1)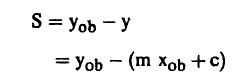 ...........
...........
ومن ثم نحصل على مجموعة من الاختلافات، أي أن:
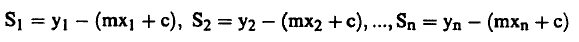
تعبر هذه المجموعة عن مدى انطباق الخط المستقيم مع القيم المقاسة. و نحصل على خط مستقيم يمر بالنقاط جميعاً عندما يساوي كل اختلاف صفراً.
دعنا نعرف الآن الدالة (c ,g(m حيث:
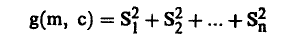
أي أن:
(2).............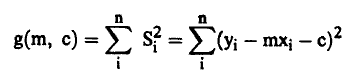
حسب مبدأ المربعات الصغرى فإن أفضل خط مستقيم يمر بالنقاط السابقة هو الخط الذي تبلغ عنده (g(m, c قيمة صفري أي أن:
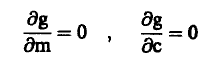
وبالتعويض من معادلة (2) نجد أن هذا الشرط يتحقق عندما:
(3).............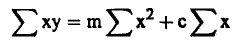
(4).............
ويحل هاتين المعادلتين يمكن ايجاد قيمة كلا من المجهولين C, m. ومن ثم نحدد افضل خط مستقيم يمر بالنقاط العملية.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|