


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 21-4-2017
التاريخ: 3-1-2022
التاريخ: 15-1-2022
التاريخ: 28-12-2021
|
التحكم في المفاعلات Contral of Nuclear Reactors
يعتبر التحكم في المفاعل واحدة من أعقد المشاكل التي تواجه شغيله، ويعتمد التحكم في المفاعل بصورة عامة على الاتزان النيوتروني به، فعندما يزداد عدد النيوترونات الناتجة عن الانشطار (Keff > 1) فإن ذلك يعني أن المفاعل أصبح فوق حرج وسوف يتضاعف عدد النيوترونات ومن ثم يتسارع معدل الانشطار إلى درجة الانفجار.. !! ما لم يوقف هذا التسارع المجنون. . . أما إذا قل معدل النيوترونات الناتجة عن الانشطار عن معدل الامتصاص والتشتت وغير ذلك من العمليات في المفاعل فإن الانشطار المتسلل سوف يتوقف (1 > Keff) ومن ثم سوف يطفىء المفاعل ويتوقف عن العمل.!! أما في لحالة الحرجة (1 = Keff) فإن معدل إنتاج النيوترونات يتزن مع معدل امتصاصها ونحصل على حالة الاستقرار. فكيف إذن يمكن التحكم في المفاعل؟.
يمكن ذلك بوضع مادة تستطيع امتصاص النيوترونات الزائدة عن الحاجة .. ويتمثل ذلك في استخدام قضبان تحكم من مواد ذات شراهية كبيرة لامتصاص النيوترونات الحرارية (كما هو الحال في معظم المفاعلات) ومن هذه المواد الكادميوم والبورون وغيرهما. وبالتالي نستطيع أن نقلل من عدد النيوترونات عندما ندخل هذه القضبان إلى أعماق كبيرة في المفاعل وذلك عندما تزداد Keff أما إذا انخفضت قدرة المفاعل عندما تقل Keff عن الوحدة - فإننا تقوم بسحب هذه القضبان إلى الخارج كي يعود المفاعل إلى حالة الاستقرار.
نبين في الجدول (1) خصائص مواد التحكم في المفاعلات.
الجدول (1)
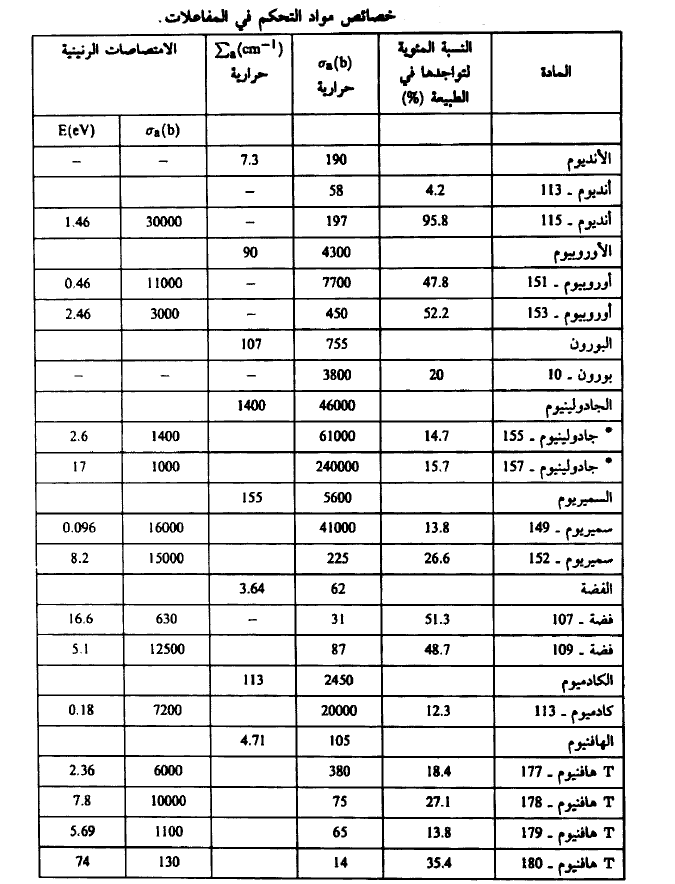
(*) هاذين العنصرين لهما عدة قمم رنينية عند طاقات تتراوح بين (2-17 م. ف)
T هاذين العنصرين لهما عدة قمم رنينية عند طاقات تتراوح بين (1.1 و 50 أف)
ولفهم عملية التحكم في المفاعلات لا بد لنا من استعرض موجز لنظرية التحكم في المفاعل. بينا أنه أثناء تشغيل مفاعل فإنه يكون في مرحلة الاستقرار الحرج حيث تكون كثافة النيوترونات ثابتة ومستقلة عن الزمن . فإذا ما حدث تغير في هذه الكثافة لسبب أو لآخر وخاصة عند بدء تشغيل المفاعل Startup أو وقف المفاعل Shutdown فإن الكثافة تتغير وتصبح دالة في الزمن إن دراسة حالة المفاعل كدالة في الزمن تعرف بحركيات (Kinetics) المفاعل كما وتعرف نظرية هذه الحالة: بنظرية حركيات المفاعل Reactor Kinetics theory حيث تعتمد هذه النظرية على كتابة ما يسمى بمعادلات حركيات النقطة Point Kinetics Equations التي تصف حالة المفاعل وتغيير Keff مع درجة حرارة المفاعل والزمن. وسوف تطبق هذه الدراسات على مفاعل متجانس حراري عاري وعلى المفاعلات بصورة عامة
سنعرف أولاً عمر الحياة للنيوترون Life Time وهو الزمن الذي يمضي بين تولد النيوترون من الانشطار وفقده من المنظومة عن طريق تفاعلات الأسر أو التسرب. وسوف نفرق هنا بين زمنين آخرين:
1- زمن التباطؤ Slowing Down Time وهو الزمن الذي يأخذه النيوترون السريع حتى يتباطؤ ويصبح نيوترون حراري.
2- زمن الانتشار Diffusion Time وهو متوسط الزمن الذي يأخذه النيوترون الحراري حتى يفقد (بتفاعل ما) من المنظومة. يبين الجدول (2) أزمنة التباطؤ والانتشار للنيوترونات الحرارية في منظومة لا نهائية لمهدئات مختلفة.
الجدول (2)
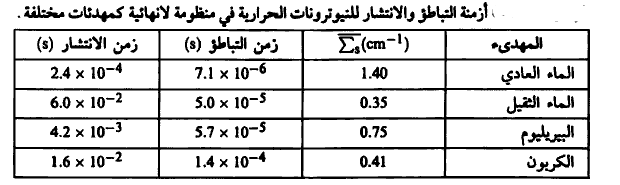
عندما يكون لدينا منظومة لا نهائية فإن النيوترونات الحرارية تفقد فقط عن طريق الامتصاص ومن ثم فإن الزمن الحراري T) Thermal Life Time) يساوي متوسط المسار الحر (λa) مقسوماً على سرعة (v) النيوترونات، أي أن:
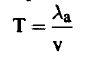
وحيث ان λa =1/∑a فإن:
(1) ..........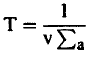
(2) .........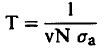
لاحظ أنه في حالة النيوترونات الحرارية (C20) فإن m/s2200 = v.
في قلب المفاعل نجد أن a∑ تساوي مساحة مقطع الامتصاص الكلي للوقود والمهدىء والشوائب. ومن ثم فإنه يمكن إثبات أن:

حيث am∑ خاصة بالمهدئ.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|