The product of a family {X_i}_(i in I)" src="https://mathworld.wolfram.com/images/equations/CategoryProduct/Inline1.gif" style="height:18px; width:35px" /> of objects of a category is an object 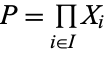, together with a family of morphisms {p_i:P->X_i}_(i in I)" src="https://mathworld.wolfram.com/images/equations/CategoryProduct/Inline3.gif" style="height:18px; width:84px" /> such that for every object 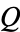 and every family of morphisms {q_i:Q->X_i}" src="https://mathworld.wolfram.com/images/equations/CategoryProduct/Inline5.gif" style="height:16px; width:69px" /> there is a unique morphism 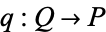 such that

for all 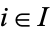. The product is unique up to isomorphisms.

In the category of sets, the product is the Cartesian product, and in the category of groups it is the group direct product. In both cases, 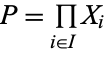, and 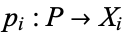 is the projection onto the 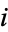th factor.

REFERENCES:

Joshi, K. D. "Products and Coproducts." Ch. 8 in Introduction to General Topology. New Delhi, India: Wiley, pp. 189-216, 1983.

Kasch, F. "Construction of Products and Coproducts." §4.80 in Modules and Rings. New York: Academic Press, pp. 80-84, 1982.

Rowen, L. "Products and Coproducts." In Ring Theory, Vol. 1. San Diego, CA: Academic Press, pp. 73-76, 1988.

Strooker, J. R. "Products and Sums." §1.5 in Introduction to Categories, Homological Algebra and Sheaf Cohomology Cambridge, England: Cambridge University Press, pp. 14-21, 1978.

اخر الاخبار

اخبار العتبة العباسية المقدسة

أساتذة المجمَع العلمي يشرفون على تحكيم المسابقة القرآنية في جامعة النهرين

قسم الشؤون الدينية ينشر صناديق مخصصة لزكاة الفطرة داخل مرقد أبي الفضل العباس (عليه السلام) وخارجه

شعبة التوجيه الديني النسوي تختتم مجالسها العبادية لإحياء ليالي القدر المباركة

قسم الشؤون الفكرية ينظم ندوة توعوية ثقافية في محافظة ذي قار

المزيد

الآخبار الصحية

تأثير اللياقة البدنية على الدماغ

تجربة سريرية تظهر فوائد اللوز للمصابين بالسمنة

اكتشاف طريقة غير متوقعة لتقليل خطر الإصابة بالسكري

خمسة مؤشرات صحية مهملة قد تنقذ حياتك

المزيد

الآخبار التكنلوجية

علماء الجيولوجيا يفكون لغز الصدع العملاق تحت الماء في المحيط الأطلسي

تحذير جديد: الاحترار العالمي يتسارع وقد نكسر حاجز 1.5 درجة قبل 2030

الصين تكشف عن ألياف كربون تفوق قوة الفولاذ بـ10 مرات

الجهاز المناعي يظهر دورا غير متوقع في صحة العظام

المزيد