


 الجغرافية الطبيعية
الجغرافية الطبيعية 
 الجغرافية الحيوية
الجغرافية الحيوية 
 جغرافية التضاريس
جغرافية التضاريس 
 الجغرافية البشرية
الجغرافية البشرية 
 الجغرافية الاجتماعية
الجغرافية الاجتماعية 
 الجغرافية الاقتصادية
الجغرافية الاقتصادية 
 الاتجاهات الحديثة في الجغرافية
الاتجاهات الحديثة في الجغرافية |
أقرأ أيضاً
التاريخ: 23-10-2017
التاريخ: 5-3-2022
التاريخ: 1-11-2021
التاريخ: 31-5-2016
|
أنماط التوزيع :
يهتم الجغرافيون بالتنظيم او التوزيع الداخلي للظاهرة ، وموقع كل عنصر من عناصر هذا التوزيع بالنسبة للعناصر الأخرى. وكان الجغرافيون يصفون التوزيع بالطريقة التي يرونها مناسبة، حسب تقديراتهم الشخصية، ولم يكن بالإمكان إعطاء تحديد واضح لخصائص التوزيع دون استخدام أدوات التحليل الحديثة.
ولا يخفى أن الجغرافي يحاول معرفة ما إذا كان التوزيع يشكل نمطاً منتظماً أم عشوائياً، فإذا كان التوزيع يشكل نمطاً منتظما، فإد ذلك يعني وجود قوى وعوامل وراء هذا النمط، أما إذا كان نمطا عشوائيا، فإن ذلك يشير إلى عامل الحظ أو المصادفة. ولما كانت الأنماط المنتظمة نتيجة عوامل وقوى متغيرة، فلا بد أن يقودنا الاهتمام بالأنماط إلى الاهتمام بالعمليات (Processes) التي تؤدي إلى تكوين هذه الأنماط بأشكالها المختلفة.
إن تحديد نمط التوزيع بطريقة موضوعية، لم يكن يهم الجغرافيين وحدهم، فقد كان أيضاً يشغل بال علماء الربة والجيولوجيا والنبات والحيوان وغيرهم من المهتمين في توزيع ظاهراتهم في المكان. وفي الواقع، إن الدور الريادي في هذا الميدان يعود إلى عالمي البيئة، (كلارك، وإيفانس Evans and Clark)، اللذين وضعا في عام ١٩٥٤ طريقة رياضية تقيس نمط التوزيع وتحدد شكله .
وتعتمد هذه الطريقة على قياس المسافة بين كل نقطة وأقرب نقطة مجاورة لها، ولذلك فقد عرفت بطريقة " الجار الأقرب " Nearest - neighbour، وذلك بهدف الوصول إلى دليل يحدد نمط لتوزيع.
والفكرة الأساسية لتحليل الجار الأقرب، هي المقارنة بين المتوسط الحسابي الفعلي لمسافة الجار الأقرب مرع بالمتوسط الحسابي النظري لمسافة الجار الأقرب مد، لعدد كبير من النقاط.
وهذا يمكن تحقيقه بسهولة باستخدام الصيغة الآتية، التي تحدد نوع التوزيع المطلوب دراسته:

حيث : ق = قرينة التوزيع.
م = المتوسط الحسابي للمسافة بين كل نقطة وأقرب نقطة مجاورة لها.
ن = عدد النقاط في المنطقة المدروسة.
ح = مساحة المنطقة المدروسة.
ك = كثافة النقاط في المنطقة المدروسة.
ومن المهم جداً، أن نلاحظ أن هذه القرينة ق تنحصر ما بين 0 و2,15 ، فإذا تجمعت جميع النقاط في نقطة واحدة فقط، فإن قيمة ق تكون صفراً، وإذا توزعت جميع النقاط بصورة منتظمة متناسقة في المنطقة المدروسة فإن قيمة ق تكون ٢,١٥ ، وإذا توزعت النقاط بصورة عشوائية فإن قيمة ق تكون ١,٠.

ويتضح مما سبق، أن المصطلحات المستخدمة محدودة، لا تزيد عن ثلاثة: متجمعة (Clustered) ومنتظمة (Regular) وعشوائية (Random)، ولكن القرينة تشمل قيماً عديدة لتحديد أنماط التوزيع المختلفة، فحينما تكون القرينة ٩ , ١ مثلا، فهذا يعني أن التوزيع يميل إلى الانتظام، ولكنه ليس تاماً. وهكذا نستطيع، بهذه الطريقة أن نتحدث بلغة أكثر دقة وموضوعية من لغتنا الوصفية السابقة.
فإذا أردنا التعرف على نمط التوزيع المكاني لمجموعة المراكز البشرية، المبينة في الشكل ٥٥، اتبعنا الخطوات الآتية:
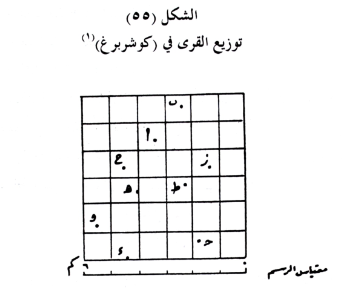
نقيس المسافة لأقرب جار، لكل مركز من المراكز البشرية ضمن المنطقة المدروسة، ثم نجمع هذه المسافات ونقسمها على عددها، فنحصل على المتوسط الحسابي للمسافات الفعلية. ويمكن الوصول إلى النتيجة نفسها، بقياس المسافات الفاصلة بين المراكز البشرية (بالسنتيمتر)، وتسجيل القياسات في مصفوفة، وتمييز الجار الأقرب بدائرة، كما هو واضح في الشكل (56).
ولا يخفى أن تغطية المنطقة المدروسة بشبكة خطوط متعامدة، تساعدنا على حساب المساحة بالكيلومترات المربعة لكل وحدة مساحية في الخريطة، وبالتالي معرفة الكثافة الحسابية (ك) في المنطقة المدروسة، وذلك بتقسيم عدد هذه المراكز على المساحة المحددة ، على النحو الآتي:

والآن، يمكن الحصول على القرينة الإحصائية لنمط التوزيع ن بنسبة المتوسط الحسابي للمسافات الفعلية إلى المتوسط الحسابي للمسافات النظرية، فنحصل على :

وهذه القرينة 1,4 تشير إلى ان التوزيع ليس عشوائيا ، او متجمعا، انما يمثل نمطا يميل إلى التناسق والانتظام ، لأن قيمة ق تزيد عن 1.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|