


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | النموذج الثنائي لمسائل البرمجة الخطيةDuality in Linear Programming:طريقة حل المسائل الثنائية بواسطة السمبلكس |
|
|
|
أقرأ أيضاً
التاريخ: 26-1-2022
التاريخ: 27-1-2022
التاريخ: 30-1-2022
التاريخ: 29-1-2022
|
طريقة حل المسائل الثنائية بواسطة السمبلكس
(Dual Simplex Method)
من خلال المقالات السابقة التي تناولت طريقة السمبلكس للمسألة الأولى تبين إذا كان  في حالة التعظيم لأي متغير أو أكثر فإن المسألة ليس له الحل الأمثل - وأن الشرط الأساسي لتحقيق الحل الأمثل أن جميع
في حالة التعظيم لأي متغير أو أكثر فإن المسألة ليس له الحل الأمثل - وأن الشرط الأساسي لتحقيق الحل الأمثل أن جميع  لكل (J).
لكل (J).
فإذا نظرنا إلى هذا الشرط من ناحية أو جهة المسائل الثنائية، فإن :

والذي يعني أن المسألة الثنائية لها حل غير موجود وهذا الشرط يتحقق عندما تكون المسألة الأولية ليس حل أمثل.
ومن جهة أخرى عندما يكون:

وهذا يعني أن المسألة الثنائية في دائرة الحل أو طريقها للحل عندما تكون المسألة الأولى لها حل مثالي.
وبناء على النتائج المدونة أعلاه فإنه يقترح حل مسألة البرمجة الخطية من جديد أو من بدايتها مرة ثانية، حيث تكون بداية المسألة ليس حل واضح ولكن في النهاية لها حل مثالي (ويمكن مقارنتها بطريقة السمبلكس الاعتيادية والتي تبدأ لها في أن لها الحل واضح وفي الأخير لا يوجد لها حل، أما الطريقة التي تختصر الحل تسمى السمبلكس الثنائي (Dual Simplex). والتي تبدأ من عدم وجود حل واضح (Infeasibility)
وتنتهي عندما يتوفر وضوح وجود للمسألة (Feasibility) وعند توفر (Feasibility) عندما يكون الحل الأمثل (Optimality). وهذا النوع من المسائل متوفر جداً في مسائل البرمجة الخطية وله أهمية كبرى، ويمكن أن يكون له عامل مساعد ومباشر في تحليل حساسية متغيرات مسائل LP.
مثال .4
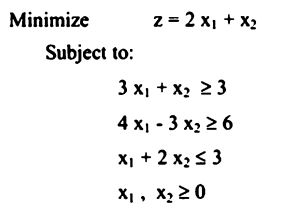
الخطوة الابتدائية تحول كل القيود من ≥ وإضافة المتغير الاحتياطي (Stack variable) للحصول على إشارة التساوي (=).
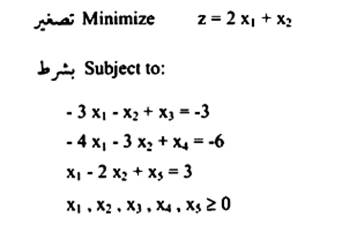
البداية بطريقة السمبلكس الاعتيادية والتي توضح أن المتغيرات الاحتياطية ,x3 ,x4 , x5 لا توفر حل واضح مادام المسألة تصغر وكل معاملات دالة الهدف تكون وهذا يعني أن الحل الأساسي للمسألة هو

فهو حل مثالي (Optimal) لكن غير منظور أو حل خيالي لأنه لا يحقق شرط  للجميع.
للجميع.
المسألة يمكن معالجة حلها بطريق السمبلكس الثنائي:

وكما هو معروف في طريقة السمبلكس - أن الطريقة تعتمد على توفر الحل المثالي - وشرط عدم الخيالية في الأرقام - حيث شرط توفر الحل المثالي تضمن توفر الحل المثالي – وعدم الخيالية تضغط على قيم المتغيرات نحو نقاط الحل ومساحته المعروفة بطرق استخدام الرسم .
شرط عدم الخيالية في فهم الأرقام (Feasibility Condition)
إن المتغير الذي يخرج من المتغيرات الأساسية يعتبر له أكبر قيمة سالبة. أما إذا كان المتغير الأساسي غير سالم فإن عمليات التغيير يجب أن تتوقف ويعتبر الحل المنظور (الغير خيالي) مثالي.
شرط وجود الحل المثالي (Optimality):
إن المتغير الذي يدخل من ضمن متغيرات الحل يتم اختياره من ضمن المتغيرات الغير أساسية في الحل (Nonbasic). تأخر النسبة بال بالنسبة للطرف الشمال أو معاملات الطرف الشمال لـ المعادلة Z إلى المعاملات المقابلة للمتغير المقترح أو المختار خروجه من المتغيرات الأساسية. إهمال أي نسبة مقامها + أو صفر - ويقرر دخول المتغير وفقاً للأقل نسبة موجبة، أما إذا كانت كل المقامات صفر أو قيمة موجبة فإن المسألة لها حل خيالي. (unfeasible)
ويعد اختيار المتغير الذي يدخل متغيرات الحل واختيار المتغير الذي يخرج يلي ذلك الحصول على تغيير الصفوف للحصول على المصفوفة الأحادية المعهودة ومنها إلى محاولة أخرى حتى الوصول إلى الحل الأمثل أو التوقف عن وجود حل.
فبالإشارة إلى الجدول السابق نلاحظ أن المتغير المختار إلى الخروج (6- = ) x لأنه يتحصل أكبر قيمة سالبة. أما المتغير التي دخل الحل فيعطي وفقاً للجدول التالي:

المتغير المرشح للدخول : لأنه مقابل إلى أقل قيمة موجبة (1/3) وبتطبيق قواعد المصفوفات للحصول على المصفوفة الأحادية التالية للمتغيرات نحصل على الجدول التالي:

الحل المدرج أعلاه مثالي ولكن خيالي حيث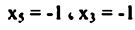
فإذا اخترنا x3 لمغادرة المتغيرات الأساسية ، فإن x1 تنطبق عليه الشروط للدخول إلى قائمة المتغيرات الأساسية والتي تعطي بالجدول التالي:
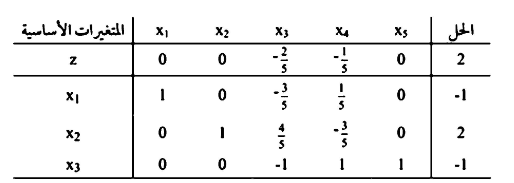
ومن الجدول الأخير يتضح ان الحل مثالي وغير خيالي.
يعتبر تطبيق طريقة السمبلكس الثنائية ذات استخدام مفيد في تحليل الحساسية. وتظهر هذه الأهمية عندما يضاف قيد جديد للمسألة بعد الحصول على الحل للمسألة بكل الإضافة. فإذا كان القيد (المضاف) لا يحقق شرط الحل الأمثل والغير خيالي فإن المسألة سيبقى لها حل مثالي ولكن خيالي. وبالتالي طريقة السمبلكس الثنائية يمكن استخدامها بدون إعادة الحل من البداية حتى تحقق شروط الحل الأمثل والغير خيالي في عدد قليل من الخطوات الحسابية.



|
|
|
|
للتخلص من الإمساك.. فاكهة واحدة لها مفعول سحري
|
|
|
|
|
|
|
العلماء ينجحون لأول مرة في إنشاء حبل شوكي بشري وظيفي في المختبر
|
|
|
|
|
|
|
قسم الشؤون الفكرية يحتفي بإصدار العدد الألف من نشرة الكفيل
|
|
|