


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 21-4-2016
التاريخ: 2023-08-07
التاريخ: 2023-10-26
التاريخ: 21-4-2016
|
لرؤية مكمن الخطأ، تخيل أن رائد فضاء على متن المركبة الفضائية ومسؤول المراقبة على الأرض يملكان ساعتين متطابقتين تماما. يفترض برائد الفضاء أن يجري تجربة بسيطة، وهي أن يصلح مصباحا موجودا على أرضية المركبة، وذلك المصباح يطلق نبضة من الضوء. تتحرك النبضة للأعلى مباشرة في اتجاه عمودي على اتجاه حركة المركبة (انظر الشكل 1-2).
وهناك تصيب النبضة على نحو دقيق هدفا مثبتًا إلى السقف. بفرض أن ارتفاع المركبة 4 أمتار، ومع تحرك الضوء بسرعته الثابتة c يجد رائد الفضاء أن الزمن الذي استغرقته هذه الرحلة 't – كما هو مقيس بساعته – يتحدد وفق المعادلة t = 4/c'
الآن، لنر كيف يبدو الأمر من منظور مسؤول المراقبة الموجود على الأرض. مع مرور المركبة فوق رأسه، يرصد هو أيضا الرحلة التي يقطعها الضوء من المصدر إلى الهدف. من منظوره، خلال الوقت الذي استغرقته النبضة للوصول إلى الهدف، يكون الهدف قد تحرك من المكان الذي كان فيه وقت انطلاق النبضة. فمن منظوره، ليس المسار عموديا، وإنما مائل (انظر الشكل 1-3). وقطعا سيكون طول هذا المسار المائل أطول من المسار المرصود من طرف رائد الفضاء. وبفرض أن المركبة تحركت بمقدار ثلاثة أمتار في الوقت الذي استغرقته النبضة في الانتقال من المصدر إلى الهدف، وباستخدام معادلة فيثاغورس، حيث 32 + 42 = 52، سنرى أن المسافة التي قطعتها النبضة للوصول إلى هدفها – من منظور مسؤول المراقبة – تبلغ 5 أمتار.
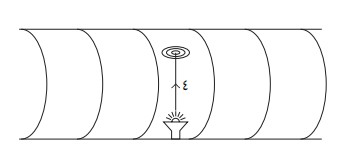
شكل 1-2: يُجري رائد الفضاء تجربة يوجه فيها نبضة من الضوء نحو هدفها؛ بحيث ينتقل الضوء في اتجاه عمودي على اتجاه حركة المركبة.
ماذا عن الوقت الذي استغرقته النبضة في رحلتها من منظور مسؤول المراقبة؟ من البديهي أن يحتسب هذا الوقت بقسمة المسافة المقطوعة، 5 أمتار، على السرعة التي رأى الضوء ينتقل بها، والتي حددناها بالفعل ومقدارها c، (وهي السرعة عينها من منظور رائد الفضاء أيضا)؛ ومن ثم، يتحدد الزمن المنقضي t وفق ساعته، من خلال المعادلة
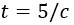
لكن هذا ليس نفس المقدار الزمني الذي وجده رائد الفضاء، والذي توصل إليه من واقع المعادلة
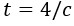 ؛
؛
ومن ثم يختلف الاثنان حول الزمن الذي استغرقته النبضة في رحلتها. من منظور مسئول المراقبة، القراءة التي سجلتها ساعة رائد الفضاء أقل مما ينبغي؛ أي إن ساعة رائد الفضاء تسير على نحو أبطأ من ساعته.
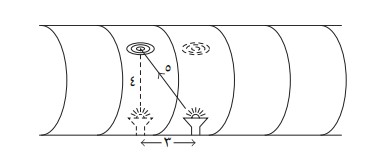
شكل 1-3: من منظور مسؤول المراقبة الموجود على الأرض، بينما تمر المركبة أعلاه، يتحرك الهدف خلال الوقت الذي استغرقته نبضة الضوء في رحلتها؛ ومن ثَم، على النبضة أن تجتاز مسارا مائلا.
ولا يقتصر الأمر على الساعة وحسب؛ فكل ما يدور على متن المركبة يتباطأ بالمعدل ذاته. فإذا لم يكن الحال كذلك، فسيكون بمقدور رائد الفضاء أن يلحظ أن ساعته تسير ببطء (مقارنة مثلا بمعدل نبضات قلبه، أو الزمن المنقضي حتى يغلي الماء داخل الغلاية... إلخ). وهذا بدوره من شأنه أن يمكنه من أن يستنتج أنه يتحرك؛ أي إن سرعته تؤثر – على نحو ما – على آلية ساعته، حيث أن هذا غير مسموح به وفق مبدأ النسبية؛ فكل أشكال الحركة المنتظمة نسبية. ولا بد من أن تسير الحياة من منظور رائد الفضاء على النحو عينه الذي تسير عليه من منظور مسؤول المراقبة؛ ومن ثم، نستنتج أن كل ما يحدث على متن المركبة الفضائية – الساعة، وآليات عمل الأجهزة الإلكترونية، وعملية تقدم رائد الفضاء في العمر، وعمليات التفكير لديه – كله يتباطأ الآن بالمعدل ذاته. وحين يرى رائد الفضاء ساعته البطيئة بعقله البطيء، لن يبدو أن هناك أي خطأ. في الواقع – في حدود علم رائد الفضاء – كل شيء داخل المركبة الفضائية يسير بسرعته الطبيعية ويبدو على ما يرام. لكن مسؤول المراقبة الموجود على الأرض هو فقط من يدرك أن كل شيء داخل المركبة يسير بتباطؤ. وهذا هو «الإبطاء الزمني». فرائد الفضاء له زمنه، ولمسؤول المراقبة زمنه، وليس الزمنان متماثلين. في ذلك المثال تعرضنا لحالة محددة؛ حالة يتحرك فيها رائد الفضاء والمركبة الفضائية مسافة 3 أمتار في الوقت الذي يقطع فيه الضوء 5 أمتار من المصدر إلى الهدف. بعبارة أخرى: تتحرك المركبة بنسبة 5/3 من سرعة الضوء؛ أي 60% من سرعة الضوء c ومع هذه السرعة المحددة وجدنا أن زمن رائد الفضاء تباطأ بمعدل 5/4؛ أي 80٪ من سرعة الضوء. من اليسير صياغة معادلة لأي سرعة مختارة  وبتطبيق نظرية فيثاغورس للمثلثABC على المسافات المبينة في الشكل 1-4، فإن:
وبتطبيق نظرية فيثاغورس للمثلثABC على المسافات المبينة في الشكل 1-4، فإن:
AC2 = AB2 + BC2
AB2 = AC2 – BC2
c²t'² = (c² - v²) t²
t'2 = (1 - v2/c2) t2
t' = t v (1 - v2/c2)
من هذه المعادلة نرى أنه كانت السرعة  صغيرة مقارنة بسرعة الضوء
صغيرة مقارنة بسرعة الضوء  ، فإن التعبير الجبري الموجود تحت علامة الجذر التربيعي يقترب من الواحد الصحيح؛ ومن ثم يتساوى الزمنان تقريبا، أو كما نعبر عنه رياضيا فإن
، فإن التعبير الجبري الموجود تحت علامة الجذر التربيعي يقترب من الواحد الصحيح؛ ومن ثم يتساوى الزمنان تقريبا، أو كما نعبر عنه رياضيا فإن
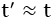 لكن مهما صغر مقدار السرعة
لكن مهما صغر مقدار السرعة  يظل تأثير الإبطاء موجودا. وهذا يعني أنه، على وجه التدقيق، في أي مرة نقوم فيها برحلة – رحلة بالحافلة مثلًا – ينبغي علينا عند الترجل منها أن نعيد ضبط ساعاتنا كي نعيد مزامنتها مع جميع الساعات وساعات الحائط الثابتة. لكن سبب عدم قيامنا بهذا هو أن ذلك التأثير طفيف للغاية. على سبيل المثال، الشخص الذي يختار العمل في قيادة القطارات السريعة طيلة حياته، سيختلف الإيقاع الزمني لديه مقارنة بمن يعملون في وظائف تتطلب منهم البقاء في الأماكن عينها، بما لا يتجاوز جزءا واحدا على المليون من الثانية عند تقاعده. وهي قيمة ضئيلة لا تستحق الانتباه إليها.
يظل تأثير الإبطاء موجودا. وهذا يعني أنه، على وجه التدقيق، في أي مرة نقوم فيها برحلة – رحلة بالحافلة مثلًا – ينبغي علينا عند الترجل منها أن نعيد ضبط ساعاتنا كي نعيد مزامنتها مع جميع الساعات وساعات الحائط الثابتة. لكن سبب عدم قيامنا بهذا هو أن ذلك التأثير طفيف للغاية. على سبيل المثال، الشخص الذي يختار العمل في قيادة القطارات السريعة طيلة حياته، سيختلف الإيقاع الزمني لديه مقارنة بمن يعملون في وظائف تتطلب منهم البقاء في الأماكن عينها، بما لا يتجاوز جزءا واحدا على المليون من الثانية عند تقاعده. وهي قيمة ضئيلة لا تستحق الانتباه إليها.
على الطرف المقابل، تنبئنا المعادلة بأنه مع اقتراب السرعة  من سرعة الضوء c، يقترب التعبير الجبري الموجود تحت علامة الجذر التربيعي من الصفر، وتميل 't لأن تكون صفرا. بعبارة أخرى: يتوقف الزمن بالنسبة لرائد الفضاء تماما. هذا يعني أنه لو تمكن رائد الفضاء من السفر بسرعة تقارب سرعة الضوء، فلن يكبر في العمر مطلقا، ومن ثم سيعيش إلى الأبد. الجانب السلبي في هذا بالطبع هو أن مخه نفسه سيتوقف بالكامل تقريبا؛ وهو ما يعني أنه لن يكون واعيا إلى أنه اكتشف سر الشباب الدائم.
من سرعة الضوء c، يقترب التعبير الجبري الموجود تحت علامة الجذر التربيعي من الصفر، وتميل 't لأن تكون صفرا. بعبارة أخرى: يتوقف الزمن بالنسبة لرائد الفضاء تماما. هذا يعني أنه لو تمكن رائد الفضاء من السفر بسرعة تقارب سرعة الضوء، فلن يكبر في العمر مطلقا، ومن ثم سيعيش إلى الأبد. الجانب السلبي في هذا بالطبع هو أن مخه نفسه سيتوقف بالكامل تقريبا؛ وهو ما يعني أنه لن يكون واعيا إلى أنه اكتشف سر الشباب الدائم.
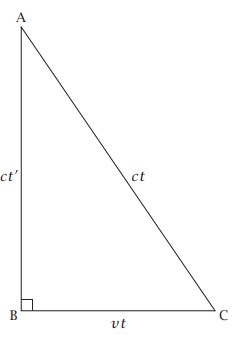
شكل 1-4: من منظور مسؤول المراقبة، BC هي المسافة التي قطعتها المركبة في الوقت الذي استغرقته نبضة الضوء في الوصول إلى هدفها، بينما AC هي المسافة التي قطعتها النبضة. اما AB فهي المسافة التي قطعتها النبضة من منظور رائد الفضاء.
كفانا نظريات. هل ينطبق هذا في الواقع العملي؟ بكل تأكيد، نعم. ففي عام 1977، مثلًا، أُجريت تجربة في مختبر سيرن في جنيف على جسيمات دون ذرية تدعى الميونات. هذه الجسيمات الدقيقة غير مستقرة، وبعد متوسط زمني قدره -106*2.2 ثوان (أي 2.2 جزء على المليون من الثانية) تتحلل إلى جسيمات أصغر. دفعت هذه الجسيمات إلى التحرك على نحو متكرر في مسار دائري قطره نحو 14 مترا، بسرعة قدرها 0.9994 من سرعة الضوء. وقد وجد أن عمر هذه الميونات أطول من عمر الميونات الساكنة بنحو 29.3 ضعفا؛ بالضبط النتيجة التي توقعناها من المعادلة التي اشتققناها، وذلك في حدود دقة قدرها جزء واحد في الألفي جزء.
وفي تجربة منفصلة أُجريت عام 1971، تم التحقق من المعادلة في إطار سرعات وهي الطائرات، وذلك بالاستعانة بساعتين ذريتين متطابقتين، وضعت إحداهما على متن طائرة، والأخرى على الأرض. ومجددا، كان هناك توافق جيد بين النظرية والنتائج. وهاتان التجربتان، إضافةً إلى تجارب أخرى لا تُحصى، تؤكد جميعها صحة معادلة الإبطاء الزمني.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|