المعامل التركيبي F_hkl هو محصلة لعدد j من الموجات مشتتة في اتجاه الانعكاس hkl بواسطة عدد j من الذرات في الوحدة البنائية كل من هذه الموجات لها سعة متناسبة مع f_j وهي معامل الاستطارة للذرة ولها زاوية طور δ تقاس بالنسبة للموجه المشتتة بواسطة إلكترونات يفترض أنها عند مركز الوحدة البنائية، ولإمكانية حساب المعامل التركيبي توجد حاجة لاستنباط معادلة تربط بين أطوار الانعكاسات وأماكن الذرات ومعاملات ميلر ومثل هذه العلاقة يمكن اشتقاقها باستخدام شكل (8-7).

شكل (7-8)

فمن تعريف معاملات ميلر، فمجموعة المستويات hkl تُقطع المحور a إلى عدد h والمحور b إلى عدد k و c إلى عدد l من الأقسام وحيث إنه يوجد فرق في الطور يساوي (360)π2 بين الانعكاسات من المستويات المتتالية لكل مجموعة hkl فمن الواضح أن الفرق في الطور لإزاحة قدرها الوحدة في اتجاه المحاور أو أي خط موازي لهذه المحاور يكون

2πh، 2πk، 2πl

على التوالي، وفي حالة الإزاحة التي تساوي جزءا من الوحدة فإن الفرق في الطور يكون أيضا جزءا من ذلك المقابل لوحدة الإزاحة، ومن الشكل يمكن استنتاج أن الفرق في الطور بين النقطتين 0،0 ،0 وw، v، u

لمجموعة المستويات hkl هو:

وبالتعويض في المعادلة (46-7) نحصل على القيمة العددية للمعامل التركيبي.

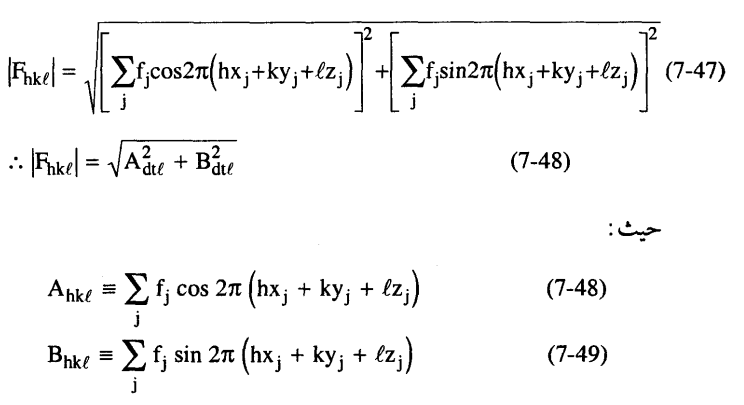
وبالمقارنة بالمعادلة (44-7) وبالرجوع للمعادلة (45-7) نجد أن زاوية الطور للموجة المحصلة.

المعامل التركيبي يمكن التعبير عنه أيضا بعدد مركب يتكون من جزء حقيقي وجزء تخيلي.