رأينا فيما قبل كيف أنه في الإمكان حساب المعامل التركيبي بمعلومية توزيع إلكتروني سواء أكان توزيعا ذريا أو توزيعا مستمرا ومن الضروري أيضا إجراء العملية العكسية ألا وهي الحصول على التوزيع الإلكتروني بمعلومية معاملات التركيب فلأن البلورات هي تركيبات دورية (periodic)؛ لذلك فإنه من الطبيعي تمثيلها بدلالة دورية periodic function، وقد وجد أن أنسب هذه الدوال هي متسلسلات ودوال الجيوب وجيوب التمام، ومثل هذه المتسلسلات تسمى متسلسلات فورییر Fourier series وأحد أشكال هذه المتسلسلات هي المتسلسلة في بعد واحد كالآتي:

حيث قيم h قيم ثابتة من الأعداد الصحيحة، x هي جزء نسبي من دورة كاملة. مثال بسيط لمتسلسلة فوريير موضح بشكل (7-10).

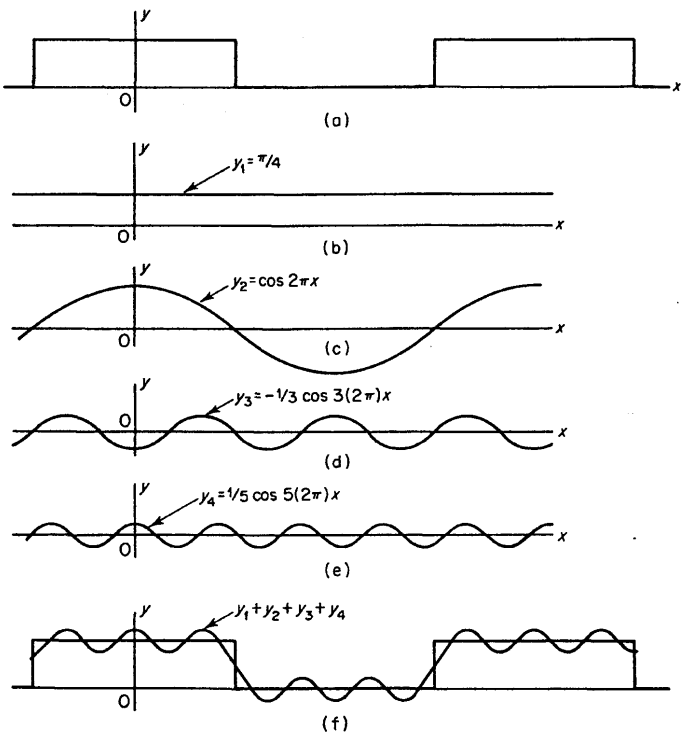
شكل (7-10)

(a) دالة دورية ذات درجات (خطوات) من (b) الى (e) رسم للاربع قيم الأولى من متسلسلة فوريير الممثلة (a)

(f) مجموع القيم الأربع الممثلة في الاشكال من b الى e لتقريب الدالة

وغالبا يكون من الأنسب تمثيل متسلسلة فوريير بدلالة الاعداد المركبة والاستعانة بالمعادلات (57-7)، (58-7)، (59-7) حيث نجد ان:

وهذا هو الشكل العام لمتسلسلة فوريير في بعد واحد في الشكل الأسى والصورة الأخرى المستخدمة في الحسابات يمكن الحصول عليها من المعادلة (62-7) وهي:

والآن لنفترض أن الكثافة الإلكترونية الدورية في الأبعاد الثلاثة لبلورة يمكن أن تمثل بمتسلسلة لفوريير في الثلاثة أبعاد مماثلة لتلك في المعادلة (72-7):

وبالتعويض بالمعادلة (74-7) في المعادلة (65-7) نحصل على:

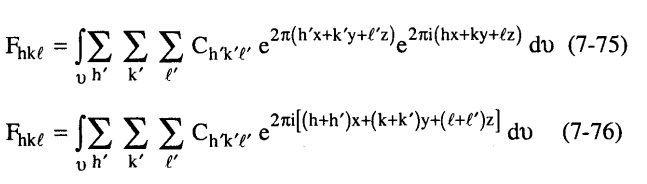
وحيث إن التكامل على دورة واحدة يساوي الصفر لكل العناصر إلا التي تكون  h- = h'، -l = l'، k' =-k عندئذ تتلاشى الصفة الدورية وتصبح:

وبمقارنة هذه المعادلة (79-7) للكثافة الإلكترونية بالمعادلة (64-7) للمعامل التركيبي نلاحظ التشابه بينهما حيث نجد أن الكثافة الإلكترونية هي تحويل فوريير (Fourier Transform) للمعامل التركيبي وكذلك المعامل التركيبي هو تحويل فوريير للكثافة الإلكترونية.

شکل آخر لمعادلة متسلسلة فوريير في الأبعاد الثلاثة يمكن الحصول عليه:

وإذا أخذنا مفكوك هذه المعادلة بدلالة الجيب وجيب التمام والأخذ في الاعتبار قانون فريدل Friedel' s law حيث يكون تأثيره هو تلاشي قيم المقادير التي تحتوي على الجيوب (sin) للمقادير F_hkl و _̅h̅k̅lF لنحصل على:

وهذا الشكل لمتسلسلة فوريير أكثر فائدة حيث نجد زاوية الطور موجودة بصفة مفردة.