


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-09-24
التاريخ: 2023-10-07
التاريخ: 24-5-2016
التاريخ: 2023-09-26
|
من المعروف أن قوى التجاذب بين أيونين مختلفي الشحنة (q ±) هي 2q/r-، أما إذا كان الأيونان متفقين في الشحنة فالقوى بينهما تنافرية وهي 2q/r+، إذا كانت المسافة بينهما هي r. وعندما تنتظم الأيونات في تركيب بلوري ما، فإن ذلك يكون عندما يتوازن أقوى تجاذب مع قوى التنافر التي تتجلى عند مسافات صغيرة بين قلبي الأيونين. أما إسهام قوى فان درفال في طاقة التماسك داخل البلورة الأيونية فيكون ضئيلا ولا يتجاوز من 1 إلى 2 في المائة. أما الإسهام الرئيسي في طاقة الترابط للبلورات فيكون كهروستاتيكيا وتسمى الطاقة عندئذ «طاقة ماديلونج».
هب أن لدينا أيونين ونرمز لهما بالرمزين i وj ، وأن طاقة التفاعل بينهما هي Uij. وتكون مجموع الطاقات Ui التي يشترك فيها الأيون (i) هي:

حيث يضم المجموع Ʃ كل الأيونات فيما عدا الحالة i =j وإذا افترضنا أن Uij هي مجموع جهد تنافري لمجال مركزي على الصورة:
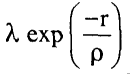
حيث ρ، λ بارامترات تجريبية مضافا إليه جهد كولومي هو 2q2/r± أي أن:
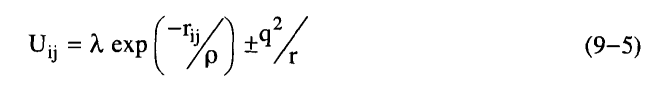
حيث تؤخذ الإشارة الموجبة (+) في حالة الشحنات المتشابهة والإشارة السالبة (–) للشحنات المختلفة. ويصف الحد التنافري حقيقة أن القشرات الإلكترونية تتصرف كما لو كانت كيانات صلبة متماسكة، وأن كل أيون يقاوم التوزيعات الإلكترونية للأيونات المجاورة. وتعتبر الشدة λ والمدى ρ من الثوابت التي يتم تعيينها من ثوابت الشبيكة وقيم الانضغاطية. ويلاحظ أننا قد استخدمنا الصيغة الأسية للتنافر بدلا من صيغة 12–R التي استخدمت من قبل في حالة الغازات الخاملة. وذلك لسهولة التعبير بها عن التنافر.
وسنتناول بلورة كلوريد الصوديوم كمثال، وإذا تغاضينا عن تأثيرات السطح فإن الطاقة الكلية للشبيكة Utot لبلورة مكونة من N جزيء أو N2 أيون، فإن:

حيث Ui هي الكمية المعرفة في المعادلة (4-9) وقد استخدمنا N بدلا من 2N لأننا لابد وأن نعد كل زوج من التفاعلات مرة واحدة (أو كل رابطة مرة واحدة). أما الطاقة الكلية في (6-9) فهي الطاقة اللازمة لتفتيت البلورة إلى أيونات منفردة يبعد بعضها عن البعض مسافات لا نهائية.
ومن المناسب هنا أن نُعرف كميات جديدة هي Pij بحيث rij = pij R، حيث R هي المسافة بين أقرب الجيران في البلورة وعلى هذا:

ولابد أن يشمل المجموع إسهام أقرب الجيران وهو العدد z. أما الرمز (±) فسيأتي ذكره بعد قليل. وتعتبر قيمة ثابت ماديلونج على جانب كبير من الأهمية في نظرية البلورات الأيونية.
وعند حدوث اتزان فإن المسافة بين الذرات يمكن تحديدها من الشرط الآتي:

والمعادلة الأخيرة هي التي تعطى مسافة الاتزان R0 عندما تكون الثوابت ρ، لقوى التنافر معروفة. يلاحظ أن المعادلات السابقة قد تم اشتقاقها على وحدات CGS، أما إذا أردنا التحويل إلى وحدات SI فعلينا وضع q2/4ε0 π بدلا من q2.
وفي بلورة مكونة من 2N أيون موزعة على مواقع محددة بمسافات الاتزان R0، فإن الطاقة الكلية للشبيكة تصبح – طبقا للمعادلتين (8-9)، (11-9) – كما يلي:

ويعرف المقدار 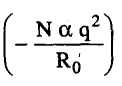 بطاقة ماديلونج، حيث تقترب قيمة ρ من 0.1R0؛ أي أن طاقة التماسك يحكمها إسهام ماديلونج. وكلما كانت قيمة ρ/R0 صغيرة كان تغير قوى التنافر حادا وكانت القوى ذات مدى قصير جدا.
بطاقة ماديلونج، حيث تقترب قيمة ρ من 0.1R0؛ أي أن طاقة التماسك يحكمها إسهام ماديلونج. وكلما كانت قيمة ρ/R0 صغيرة كان تغير قوى التنافر حادا وكانت القوى ذات مدى قصير جدا.
وفيما يلي بعض القيم النموذجية لثابت ماديلونج لبعض البلورات الأيونية الشائعة. وقد حسبت على أساس أن الشحنات أحادية ومنسوبة إلى مسافة أقرب الجيران:
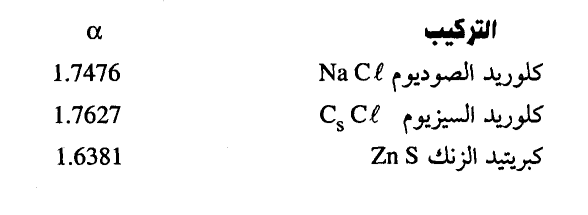



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
العتبة العباسية تبحث سبل التعاون مع شركة التأمين الوطنية
|
|
|