


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 1-2-2022
التاريخ: 2023-10-21
التاريخ: 2-2-2023
التاريخ: 7-2-2022
|
عندما لاحظ رذرفورد من خلال تجربة بعثرة جسيمات ألفا بأن هناك مجموعة من الجسيمات نفذت وأخرى انحرفت بزوايا صغيرة، وعدد قليل منها انحرف بزوايا كبيرة جدا، وعدد أخر قليل جدا ارتد إلى الوراء، استنتج من ذلك وجود جزء مركزي تتجمع فيه الشحنة الموجبة ويمثل معظم كتلة الذرة. يطلق على ذلك الجزء اسم (النواة) nucleus.
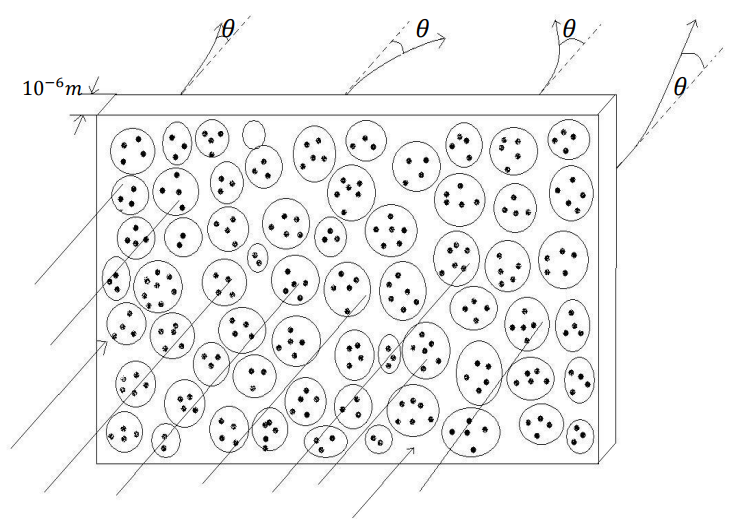
شكل (3–2)
انحراف جسيمات ألفا بزوايا مختلفة عند مرورها بصفيحة من الذهب.
لمعالجة نموذج رذرفورد، سنفترض أن كتلة النواة أكبر بكثير من كتلة جسيمات ألفا، وذلك حتى لا تغير النواة مكانها أثناء التنافر لكهربائي بينها وبين جسيمات ألفا. هذا الافتراض يجعل طاقة الحركة لجسيمة ألفا Ti مساوي لطاقة الحركة النهائية Tf:
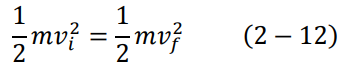
يوضح الشكل (4–2) انحراف جسيمة ألفا عند مرورها بالقرب من النواة. يتخذ مسار الجسيم شكل قطع زائد hyperbola. تعطى العلاقة الرياضية بين الزاوية θ ومعامل التصادم b بالعلاقة التالية:
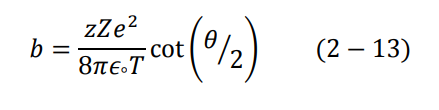
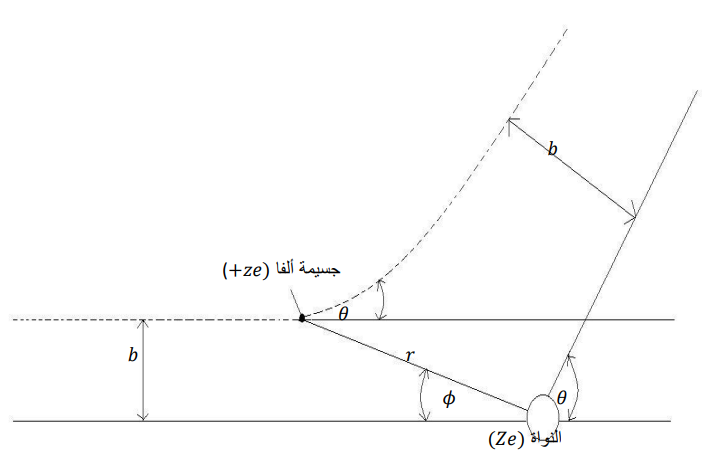
شكل (4-2)
يتخذ جسيم ألفا مسار قطع زائد بعد تفاعله مع النواة.
يبين الشكل (5-2)، أن جسيمات ألفا التي يكون معامل تصادمها يساوي b، تنحرف بزاوية قدرها θ (المسار 1) والجسيمات التي يكون معامل تصادمها أقل من b تنحرف بزاوية أكبر من θ (المسار 2) والتي يكون معامل تصادمها أكبر من b تنحرف بزاوية أصغر من θ (المسار 3) وكلما زادت قيمة المعامل b تصغر قيمة الزاوية θ، حتى يمر الجسيمة بخط مستقيم دون أي انحراف (المسار 4) بناء على ذلك يمكن تعريف معامل التصادم على انه أصغر مسافة يقتربها الجسيم من النواة دون أن يتأثر كهربائيا بها.
أن معامل التصادم لا يمكن التحكم به تجريبيا، لذلك راح رذرفورد يبحث عن علاقة أخرى يمكن اختبارها تجريبيا.
بالعودة إلى الشكل (5-2) نجد أن جميع الجسيمات التي تسقط ناحية النواة وتنحرف بزاوية θ أو أكبر، تقع جميعها في نطاق دائرة مساحتها:
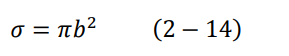
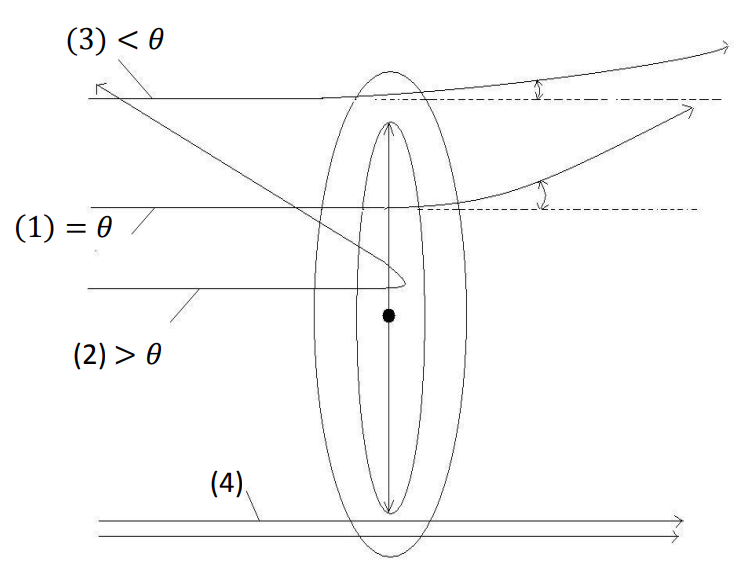
شكل (5–2)
العلاقة بين b وθ.
وتسمى σ بالمقطع العرضي cross section.
لو افترضنا أن سمك الصفيحة المعدنية التي تسقط إليها الجسيمات ومساحتها A، وكثافتها ρ، وكتلة المول M، عندها يكون حجم الرقاقة المعدنية يساوي At، وكتلتها ρAt، وعند المولات ρAt/M، ويكون في النهاية عدد الذرات في وحدة الحجم من القطعة المعدنية هو:
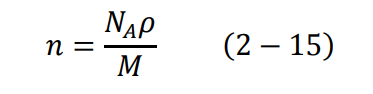
حيث NA عدد أفوجادرو Avogadro's number (عدد الذرات في المول الواحد) ويساوي 1–NA = 6.022 * 1023 mole. يوجد لدينا في الصفيحة المعدنية ذرات كثيرة جدا، ولكل واحدة من هذه الذرات مقطع عرضي σ. يعطى المجموع الكلي للمقاطع المستعرضة كالتالي:

إن النسبة بين عدد جميع جسيمات ألفا والتي تنحرف بزاوية θ أو اكبر منها، وبين الجسيمات ذاتها هي النسبة بين المساحة Aº. ومساحة الصفيحة المعدنية A. باستخدام المعادلة (13–2) و(14–2) و (16–2) نجد أن تلك النسبة هي:
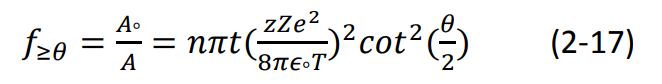
عندما يتغير معامل التصادم b في التجربة بين المدى b + db تكون عندئذ زوايا التبعثر للجسيمات في المدى θ وdθ + θ، كما هو موضح بالشكل (6-2) يحسب عدد الجسيمات في المدى θ وdθ + θ بتفاضل المعادلة (17–2) بالنسبة ل θ، حيث نجد:
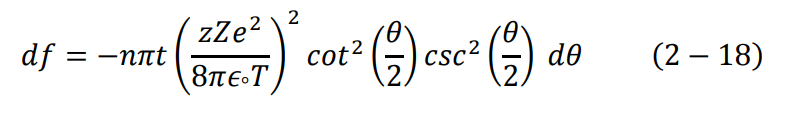
و يمكن إهمال الإشارة السالبة هنا، فهي تبين فقط التناسب العكسي بين θ وb.
يبين الشكل (7–2) تبعثر جسيمات ألفا في المدى θ وdθ + θ من الأعلى والأسفل، مما يشكل في النهاية مخروط زاويته .2θ في التجربة يوضع كاشف كروي الشكل في المدى θ وdθ + θ وذلك حتى تسقط جسيمات ألفا بشكل عمودي على الكاشف.
تعتمد احتمالية وصول جسيمات ألفا إلى الكاشف الكروي على df والتي تعطي احتمالية تبعثر جسيمات ألفا خلال الحلق الذي نصف قطره θ r sin، وعرضه dθ . تعطى مساحة الحلق بالعلاقة التالية:
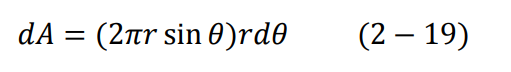
ولكي نحسب معدل الجسيمات المبعثرة إلى الكاشف، يجب أن نقوم بحساب نسبة الاحتمالية df الى مساحة الحلق dA. باستخدام المعادلات (18-2) و(19–2) وباستخدام بعض العلاقات المثلثية نحصل أخيرا على:
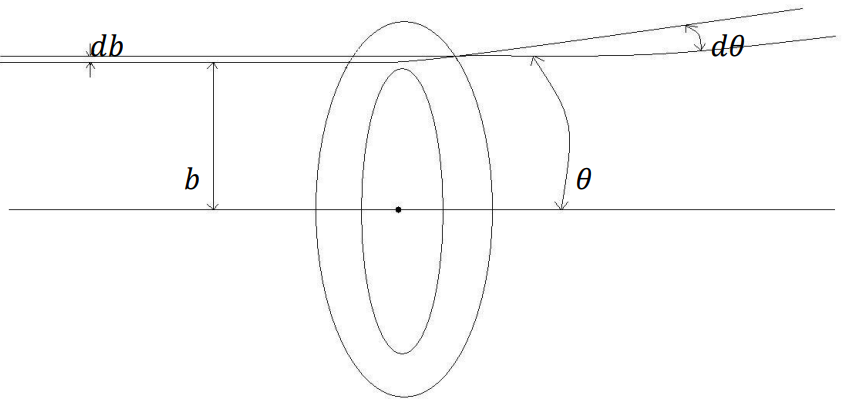
شكل (6-2)
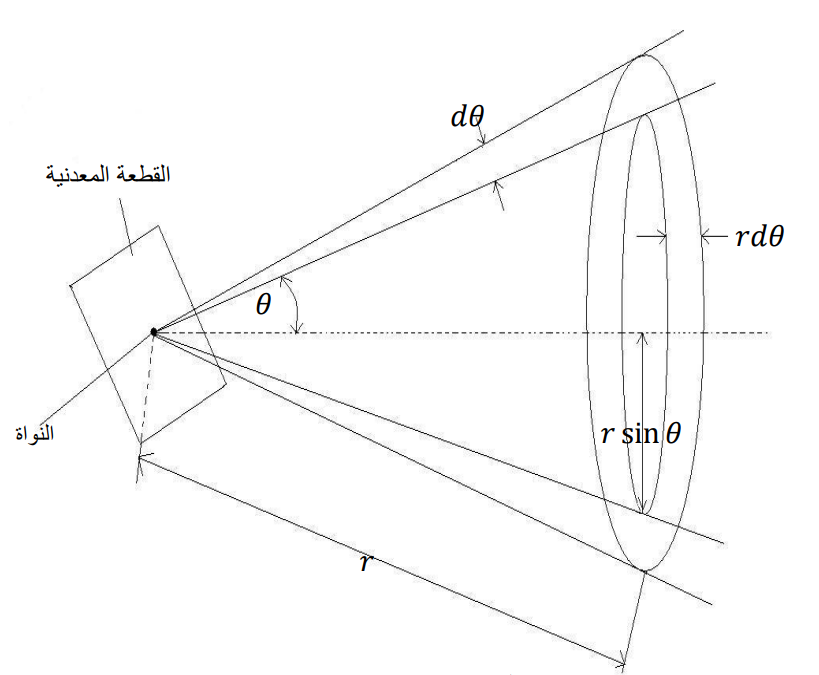
شكل (7–2)
تتجمع جسيمات ألفا على شكل حلق، ويمكن الكشف عن معدل جسيمات ألفا في المدى θ وdθ في موقع الكاشف الكروي.
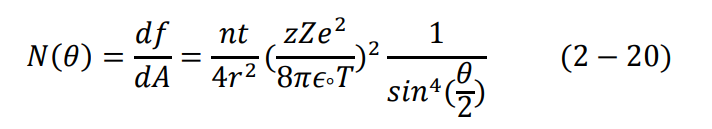
وتعرف هذه المعادلة الشهيرة بدستور رذرفورد للاستطارة. نلاحظ من هذه المعادلة ما يلي أولا: عدد الجسيمات التي تسقط على الكاشف، تتناسب طرديا مع سمك القطعة المعدنية t. ثانيا: هناك تناسب طردي بين (θ)N ومربع العدد الذري Z. ثالثا: هناك تناسب عكسي بين (θ)N وطاقة الحركة T. وبالفعل تم التأكد من هذه النتيجة عن طريق استخدام رقاقة نحيفة من المايكا mica لإبطاء سرعة جسيمات ألفا. رابعا: هناك تناسب عكسي بين (θ)N و(θ/2)sin4 ، كما نرى في الشكل (8–2) حيث العلاقة العكسية بينهما عند ثبوت جميع العوامل الأخرى.
منذ أن بدأنا بمعالجة نموذج رذرفورد كان حديثنا منصبا على الجسيمات التي تعبر القطعة المعدنية. لكن ماذا عن الجسيمات القليلة جدا والتي ترتد إلى الوراء (عندما تكون 0 = b). لقد رأينا من المعادلة (12–2) أن طاقة الحركة الابتدائية تساوي طاقة الحركة النهائية، ولكن في حال الجسيمات التي تقترب رأسا من النواة، تبدأ عندها طاقة الحركة بالانخفاض تدريجيا حتى يقترب الجسيم إلى أقرب نقطة من النواة في هذه اللحظة تتحول كل طاقة الحركة للجسيمات إلى طاقة وضع U، ولا يتم ذلك إلا في حالة 0 = b، أما اذا كانت b صغيرة جدا فأن طاقة الحركة للجسيمات لا تنعدم ولكن تصبح صغيرة جدا.
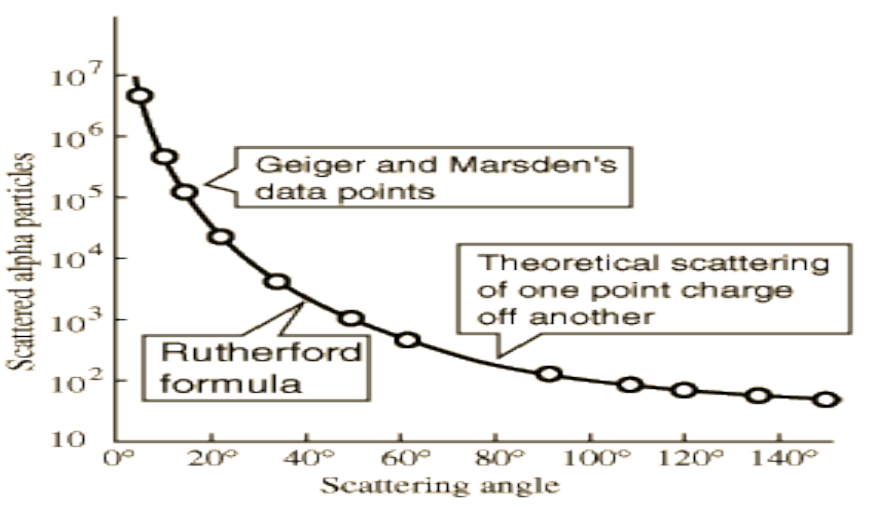
شكل (8–2)
العلاقة العكسية بين (θ/2)sin4 و(θ)N حيث تتناسب بدقة مع معادلة رذرفورد.
لو اعتبرنا أن الجهد الابتدائي يساوي صفر (0 = Ui) وذلك لأن الجسيم بعيد جدا عن النواة واعتبرنا كذلك أن 0 = b، تصبح طاقة الحركة النهائية (0 = Tf) وباستخدام قانون حفظ الطاقة تصبح المعادلة (12–2) كالتالي:
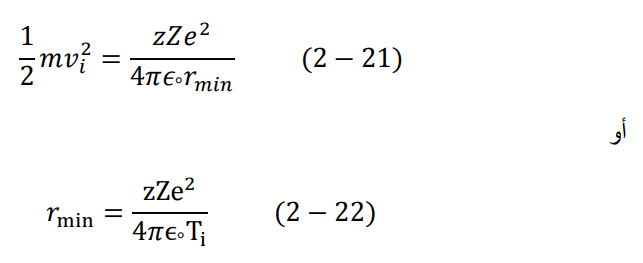
وتعطي هذه المعادلة أصغر مسافة يقتربها جسيم من النواة ثم يرتد إلى الخلف (rmin).
حتى الآن يبدو نموذج رذرفورد رائع جدا، وقد أجرى جايجر ومارسدن سلسلة من التجارب الكثيرة جدا تتفق بصورة ممتازة مع كل المعادلات الموجودة في هذا النموذج. لكن في هذا النموذج لم نذكر ولا حتى كلمة واحدة بخصوص الالكترونات لا يمكن أن تكون الالكترونات في هذا النموذج منتشرة وساكنة كما هو الحال في نموذج طومسون، لان الشحنة الموجبة لم تعد الآن منتشرة بشكل مستمر فهي الآن مرتكزة في مركز الذرة وهذا يجعل الالكترونات تسقط إلى النواة إذا ما اعتبرناها منتشرة وساكنة كما في نموذج طومسون، وبالتالي ينهار شكل الذرة كليا.
لتجنب تلك الصعوبة اقترح رذرفورد أن الالكترونات تدور بشكل دائري حول النواة تماما كدوران الكواكب حول الشمس. ولما كانت الكواكب لا تسقط في أثناء دورانها حول الشمس، بسبب قوة الطرد المركزي، افترض رذرفورد أن ذلك أيضا صحيح في حال الالكترونات، حيث تتعادل قوة الطرد المركزي مع الجذب الكهربائي للنواة وبالتالي لا ينهار الإلكترون على النواة.
لكن افتراض رذرفورد حول حركة الالكترونات الدائرية يتعارض بشكل مباشر مع واحد من المبادئ الأساسية في النظرية الكهرومغناطيسية. ينص هذه المبدأ على أن كل الأجسام المشحونة المتسارعة تصدر إشعاعا كهرومغناطيسيا، وهذا بدوره يؤدي إلى نقصان طاقة الإلكترون تدريجيا وبالتالي إلى سقوطه بشكل حلزوني متسارع نحو النواة، كما هو موضح بالشكل (9-2). كذلك وحسب النظرية الكهرومغناطيسية، يجب أن يكون تردد الإشعاع الكهرومغناطيسي المنطلق من الالكترونات مساويا لتردد مدار الإلكترون. ولما كانت طريقة دوران الإلكترون الحلزونية متصلة، يجب أن يكون طيف الإشعاع 3 بمختلف تردداته متصل أيضا. ولكن في الحقيقة هذا غير ملاحظ تجريبيا، إذ ما تم ملاحظته من التجارب هو ظهور الطيف على شكل خطوط متقطعة وليست متصلة.
لذلك وعلى الرغم من النجاح الباهر لنموذج رذرفورد في تفسيره لشكل الذرة وتجنب الصعوبات التي واجهت نموذج طومسون لم يستطيع نموذجه التغلب على تلك العقبتان الأخيرتان. كان لا بد من تفسير لهذه المشاكل حتى يكتمل شكل الذرة الأنيق.
في تلك الظروف كان هناك شاب مغمور يشق طريقه عبر البحار قادما من كوبنهاغن إلى مانشستر، وقد حصل لتوه على شهادة الدكتوراه، وكان موضوع أطروحته عن نموذج طومسون. حيث اكتشف خطأ رياضيا في حسابات طومسون انضم في خريف عام 1911 إلى فريق رذرفورد الذي يضم نخبة من الفيزيائيين الشبان، وبدأ أبحاثه هناك واهتم بتفسير خطوط الأطياف الذرية التي عجز نموذج رذرفورد عن تفسيرها. يدعى ذلك الشاب نیلز بور Niels Boher.
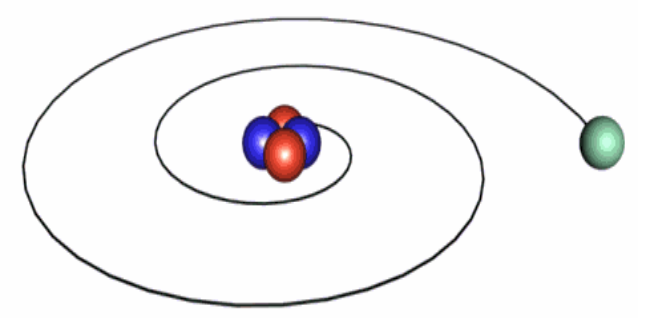
شكل (9–2)
انهيار الإلكترون بشكل حلزوني متسارع داخل النواة، مما يؤدي بالنهاية إلى انهيار شكل الذرة بالكامل.
_____________________________________________________
هوامش
[3] سوف نتكلم بالتفصيل عن خطوط الأطياف الذرية في الجزء القادم من هذا الفصل.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|