


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 24-10-2020
التاريخ: 29-10-2020
التاريخ: 28-11-2019
التاريخ: 2023-11-20
|
جدتي وجاليليو جاليلي
علم الفيزياء علم تجريبي في جوهره والقياسات وما يتخللها من ارتياب هي صميم كل تجربة وكل اكتشاف وحتى أعظم الفتوح النظرية في الفيزياء تُقدَّم في شكل تنبؤات عن مقادير يمكن قياسها. فلننظر على سبيل المثال إلى قانون نيوتن الثاني F = ma (القوة تساوي الكتلة مضروبة في التسارع) والذي قد يُشكل أهم معادلة في الفيزياء، أو لننظر إلى معادلة آينشتاين 2E = mc (الطاقة تساوي الكتلة مضروبة في مربع سرعة الضوء)، وهي أشهر معادلات الفيزياء قاطبة كيف للفيزيائيين أن يعبروا عن العلاقات إلا من خلال المعادلات الرياضية المتعلقة بالمقادير القابلة للقياس، مثل الكثافة والوزن والطول والشحنة والجاذبية والحرارة والسرعة؟
سوف أقر هنا بأنني منحاز بعض الشيء؛ لأن بحث أطروحة الدكتوراه الذي أنجزته قوامه قياس أنواع مختلفة من الاضمحلال النووي بدرجة عالية من الدقة، وأن إسهاماتي في السنين الأولى من بزوغ نجم علم فلك الأشعة السينية قد تأتت من قياسات أشعة سينية عالية الطاقة أتت إلينا من مسافة تقدر بآلاف السنين الضوئية. لكن بكل بساطة لا فيزياء بدون قياسات والحقيقة التي لا تقل أهمية عن ذلك هي أنه لا قياسات ذات دلالة لا يحيط بها الارتياب.
والواقع أنك أيها القارئ تعتمد على قدر كبير من الارتياب طوال الوقت دون أن تدرك ذلك؛ فعندما يُبلغك مصرفك برصيد حسابك لديه، فإنك ترتاب في وجود خطأ قد يقل عن نصف بنس؛ وعندما تبتاع قطعة ملابس عبر شبكة الإنترنت فإنك تتوقع أنها ستناسبك ولن يختلف قياسها عن قياسك إلا بقدر يقل عن قياس واحد. فمثلا إذا ابتعت بنطالا قياسه 34 قد يتباين قياسه بمقدار 3 بالمائة في منطقة الخاصرة فيأتي قياسه الحقيقي 35 فينزل حتى فخذيك وقد يأتي قياسه الحقيقي 33 ويجعلك تتساءل كيف زاد وزنك إلى ذلك الحد.
ومن الضروري أيضًا أن تُستخدم وحدات مناسبة للتعبير عن القياسات. ولنأخذ مثالا على ذلك تلك المهمة الفضائية التي استغرقت أحد عشر عامًا وتكلفت 125 مليون دولار – مهمة مركبة المريخ المناخية المدارية – والتي انتهت نهاية كارثية بسبب الخلط الذي حدث بين الوحدات. فقد استخدم أحد فريقي المهندسين الوحدات المترية بينما استخدم الفريق الآخر الوحدات الإنجليزية، ونتيجة لهذا انتهى الحال بالمركبة عام 1999 أن استقرت في مركز الغلاف الجوي للمريخ بدلا من أن تستقر في مدار ثابت.
أستخدم الوحدات المترية في الأغلب وذلك لأن غالبية العلماء يستخدمونها. لكني استعين أيضًا بوحدات إنجليزية مثل البوصة والقدم والميل والرطل بين حين وآخر. ففيما يتعلق بدرجة الحرارة، استخدمتُ مقياسي السيلزيوس والكلفن (الذي يساوي درجة سيلزيوس زائد 273.15) واستخدمتُ أيضًا مقياس فهرنهايت في بعض الأحيان رغم أنه ما من فيزيائي يتعامل مع درجات الحرارة بمقياس فهرنهايت.
ولأنني أُقدّر الدور المحوري الذي تلعبه القياسات في الفيزياء فإنني أتشكك في النظريات التي لا يمكن التحقق منها عن طريق القياسات. لنتأمل نظرية الأوتار أو تلك النظرية المتصلة بها والأكثر تفصيلا، نظرية الأوتار الفائقة، وهما أحدث الجهود التي قام بها العلماء النظريون في سبيلهم لإيجاد «نظرية كل شيء». لم يتوصل العلماء النظريون بعد، رغم أن من بينهم علماء أفذاذ يعملون على نظرية الأوتار، إلى تجربة واحدة أو توقع واحد قادر على اختبار أطروحات نظرية الأوتار. ولا يمكن التحقق من أي شيء في نظرية الأوتار تجريبيا، حتى الآن على الأقل. وهو ما يعني أن نظرية الأوتار لا تتمتع بأية قوة تنبؤية، وهو الأمر الذي حدا ببعض الفيزيائيين، من أمثال شيلدون جلاشو، الأستاذ بهارفارد، أن يتساءلوا عما إذا كانت تلك النظرية تمتُ للفيزياء بصلة من الأساس.
إلا أن لنظرية الأوتار بعض المناصرين الأذكياء البلغاء واحد من هؤلاء هو براين جرين صاحب الكتاب والبرنامج التلفزيوني على قناة بي. بي. إس. اللذين يحملان ذات العنوان «الكون الأنيق» (وقد حللت ضيفًا في فقرة قصيرة من هذا البرنامج) ويشتركان في جمالهما وسحرهما. ومن أولئك أيضًا إدوارد ويتن، صاحب نظرية إم، وهي النظرية التي وحدت خمس نظريات أوتار مختلفة، وافترضت وجود أحد عشر بعدا للفضاء، لا نرى نحن منها، بصفتنا كائنات متدنية الرتبة إلا ثلاثة. وهي أطروحات جامحة باعثة على التأمل.
لكن تلك النظرية لا تفتأ تذكرني بجدتي لأمي، وقد كانت سيدة عظيمة في جعبتها الكثير من الأقوال والعادات التي كانت ستجعل منها عالمة بالسليقة. كثيرًا ما قالت لي جدتي أقوالا على غرار: إنك عندما تقف تصير أقصر قامة منك عندما تستلقي. ولكم أحب أن أدرّس هذا القول لطلابي؛ ففي اليوم الأول من الفصل الدراسي أعلن لهم أنني في إطار التكريم لجدتي سوف أضع هذا المفهوم الغرائبي تحت الاختبار. وهو الأمر الذي يجعل الطلبة في قمة الحيرة، وأكاد أسمع أفكارًا تدور في رؤوسهم من قبيل: «تقصر القامة وقوفًا عنها عند الاستلقاء؟ هذا مستحيل».
ويمكنني تفهم عدم اقتناعهم، فبالقطع لو كان هناك أي اختلاف في الطول بين وضعي الاستلقاء والوقوف فسيكون اختلافًا طفيفا جدًّا. فلو بلغ الفارق قدمًا كاملة فسنلاحظ هذا، أليس كذلك؟ حينها ستنهض من فراشك فتسمع صوت انكماش قامتك، وتقصر بمقدار قدم واحدة. لكن لو كان الفارق قدره 0.1 من السنتيمتر (أي 25/1 من البوصة) فلن نلاحظه. ولذلك فإنني خمنتُ أنه لو كانت جدتي محقة، فإن الفارق لن يتجاوز سنتيمترات قليلة، أو ربما بوصة واحدة على الأرجح.
ولكي أجري تجربتي تلك كان عليّ بالطبع أن أقنع طلبتي بالارتياب الذي يشوب قياساتي. لذلك فقد بدأتُ بقياس قضيب من الألمنيوم في وضع عمودي – بلغ طوله حوالي 150.0 سنتيمترًا – وطلبت منهم أن يتفقوا معي على أنني قادر على القياس بمقدار ارتياب يزيد أو ينقص عن جزء من عشرة أجزاء من السنتيمتر. وبهذا يصير القياس العمودي 150.0 ± 0.1 سنتيمتر. ثم قستُ طول القضيب في الوضع الأفقي وجاء قياسه 149.9 ± 0.1 سنتيمتر وهو القياس الذي يتفق مع القياسات العمودية – في إطار مقدار الارتياب في القياسات.
ما الذي غنمته من قياس قضيب الألمونيوم في كلا الوضعين؟ غنمتُ الكثير في الواقع. أولا أظهرت عمليتا القياس قدرتي على قياس الطول بقدر من الدقة يبلغ نحو 0.1 من السنتيمتر (ميليمتر واحد). لكن الأمر الذي لا يقل عن ذلك أهمية هو رغبتي في أن أثبت لطلابي أنني لا أمارس ألاعيب عليهم؛ لنفترض مثلا أنني أعددت مسطرة قياس «مجهزة مسبقا» خصوصًا لقياساتي الأفقية، ألا يوصف ذلك بالغش والخداع. لكنني عندما أثبت أن طول قضيب الألمنيوم متساو في الحالتين، فقد أظهرت نزاهتي العلمية بدليل لا يقبل الشك.
بعد ذلك، كنتُ أطلب متطوعًا أقيس طوله واقفًا ثم أدون ذلك الرقم على لوح الكتابة الأسود – 185.2 سنتيمترًا (أي ما يزيد عن ستة أقدام بقليل) يزيد أو ينقص بالطبع بمقدار 0.1 سنتيمتر على سبيل حساب الارتياب. ثم أساعد ذلك المتطوع على الاستلقاء على مكتبي داخل المُعدّة التي أستخدمها في القياس، والتي تبدو كمسطرة قياس عملاقة من طراز ريتز وهي المسطرة الخشبية التي تستخدم في متاجر الأحذية، غير أن الجسد كله في حالتنا تلك يحل محل القدم. في هذه الأثناء آخذ في المزاح معه بشأن إذا ما كان مرتاحًا في هذا الوضع وأهنئه على التضحية التي يبذلها في سبيل العلم، وهو ما يجعله قلقًا بعض الشيء. ماذا أحمل في كم قميصي؟ من كم قميصي أخرج قطعة خشبية مثلثة أضعها فوق رأسه، وبينما هو راقد أدون رقمًا جديدًا على لوح الكتابة. والآن صار لدينا رقمان كل منهما به نسبة من الارتياب تُقدر بـ 0.1 سنتيمتر. إذن، ما النتيجة؟
هل ستندهش عندما تعلم أن القياسين يتباينان بفارق قدره 2.5 أي ما يزيد أو ينقص عن 0.2 سنتيمتر بالطبع؟ هنا اضطررتُ لأن أخلص لكون طوله راقدًا يتجاوز طوله واقفا بـ 2.3 سنتيمتر على الأقل (نحو 0.9 من البوصة). وهنا أعود إلى طالبي المستلقي وأعلن أنه أطول بنحو بوصة كاملة وهو راقد عنه وهو واقف ثم أعلنها جهرًا – وهو أفضل ما في الأمر – أن «جدتي كانت على حق، وهي دائمًا على حق».
هل تتشكك في الأمر؟ الواقع أنه قد اتضح أن جدتي تفوق معظمنا في العلم. فإننا عندما نقف تضغط الجاذبية الأرضية تلك الأنسجة اللينة الموجودة بين فقرات عمودنا الفقري، أما عندما نستلقي فيحدث أن تتمدد أعمدتنا الفقرية. قد تبدو لك تلك المعلومة منطقية عندما تسمعها، لكن هل كان بإمكانك التنبؤ بها؟ الواقع أنه حتى علماء ناسا لم يأخذوا هذا التأثير بعين الاعتبار أثناء تخطيط أولى البعثات الفضائية. فقد اشتكى رواد الفضاء في هذه البعثة من أن حللهم الفضائية ضاقت عليهم عندما وصلوا إلى الفضاء. وقد أظهرت الدراسات التي أجريت في وقت لاحق خلال بعثة سكاي لاب أن رواد الفضاء الستة الذين أخذت قياساتهم ازدادوا طولا بمقدار 3 في المائة– أي ما يزيد قليلا عن بوصتين إذا كان طولك ستة أقدام. لذا فقد صارت حلل رواد الفضاء اليوم تصمم باتساع إضافي يستوعب هذه الزيادة في الطول.
هل أدركت مدى فائدة القياسات؟ وفي ذات الصف الذي أُثبتُ فيه أن جدتي كانت على حق أجد متعة كبيرة في قياس بعض الأشياء الغريبة؛ سعيا مني لاختبار اقتراح طرحه جاليليو جاليلي رائد علم الفلك والعلم الحديث، والذي طرح على نفسه ذات يوم السؤال التالي: «ماذا لو كان حجم أضخم الثدييات أكبر بكثير من حجمها الذي نعرفه؟»؛ وكانت إجابته عن السؤال الذي طرحه أن لو كانت الثدييات أثقل وزنا مما هي عليه، لتكسرت عظامها عندما قرأتُ عن هذا الأمر أثار فضولي، ودفعني للتحري عن صحة كلامه. لقد بدت إجابته بديهية لكنني أردتُ التحقق منها.
كنت أعلم أن عظام الفخذ في الثدييات تتحمل معظم وزنها، لذلك فقد قررتُ إجراء قياسات مقارنة بين عظام أفخاذ ثدييات مختلفة. لو كان جاليليو محقا فإن عظمة الفخذ في الثدييات الضخمة لن تكون بالقوة الكافية التي تحمل بها وزن الحيوان. لقد أدركتُ بالطبع أن قوة عظمة الفخذ لدى الثدييات تتوقف على مدى سمك تلك العظمة؛ فالعظام الأكبر سمكا قادرة على حمل وزن أكبر، ذلك أمر بديهي. وكلما كان الحيوان أكثر ضخامة احتاج إلى عظام أكبر سمكا.
كما أن عظمة الفخذ تكون أطول كلما ازداد الحيوان ضخامة بالطبع، واستنادًا على تلك الحقيقة أدركتُ أنني إذا قارنت بين طول عظمة فخذ الحيوان الثدي وسمكها في مقابل وزنه حينها فسأستطيع اختبار فكرة جاليليو. من الحسابات التي أجريتها والتي كانت من التعقيد لدرجة أنني لا أريد الخوض فيها هنا خلصت إلى أنه لو كان جاليليو محقًا فإنه كلما ازدادت الثدييات ضخامة فلا بد أن سمك عظام فخذها يزيد بسرعة تفوق زيادة طولها. من حساباتي وصلت إلى أنه لو كان حيوان ثدي ما يفوق حيوانًا آخر في ضخامته بخمسة أضعاف، فلا بد أن تكون عظمة فخذه أطول من عظمة فخذ الآخر بخمسة أضعاف ومن ثم لا بد أن سمك عظمة فخذه أكبر من سمك نظيرتها لدى الحيوان الآخر إحدى عشرة مرة.
يعني هذا أنه عند مرحلة ما سيصبح سمك عظمة الفخذ مساويا لطولها أو أكبر منه، وهو ما سيؤدي إلى تكوينات جسدية غير منطقية على الإطلاق. هذه الثدييات، ولا شك، لن تكون الأصلح للبقاء، وهذا هو السبب في أن للثدييات حجم أقصى لا تتعداه.
وهكذا تكهنتُ بأن السمك يزيد بوتيرة أسرع من وتيرة زيادة الطول. وهنا بدأت الإثارة.
ذهبت إلى جامعة هارفارد التي فيها تشكيلة جميلة من العظام، وطلبت منهم عظام فخذ لراكون وحصان. واتضح لي أن الحصان أضخم من الراكون بأربعة أضعاف، وتأكد لي أيضًا أن عظمة الفخذ لدى الحصان (42.0 ± 0.5 سنتيمتر) أطول من نظيرتها لدى الراكون بثلاث مرات ونصف (12.4 ± 0.3 سنتيمتر). إلى الآن تسير الأمور بشكل جيد؛ لذلك فقد أدخلت هذه الأرقام في معادلتي، وتوقعتُ أن تكون عظمة فخذ الحصان أكثر سمكا من مثيلتها لدى الراكون بما يزيد عن ست مرات بقليل. لكنني عندما قستُ السُّمك (بنسبة ارتياب تبلغ نحو نصف سنتيمتر لدى الراكون و2 سنتيمتر لدى الحصان) وجدتُ أن سُمك عظمة الحصان يبلغ خمس مرات سمك عظمة الراكون أي ما يزيد أو ينقص عن نسبة 10 بالمائة، وهو ما رجح كفة جاليليو بعض الشيء. لكنني قررتُ أن أزيد قدر البيانات وأضيف إليها ثدييات أصغر حجمًا وأخرى أكبر حجما. لذا فقد عدتُ إلى هارفارد فأعطوني ثلاث عظمات أخرى لظبي وفأر كيسي وفأر عادي. وكان هذا شكل العظام وهي مصفوفة بجوار بعضها:
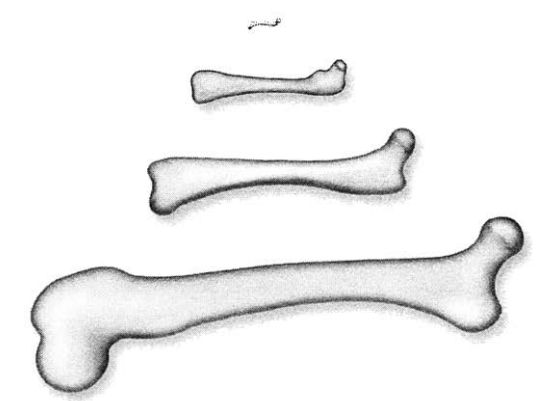
أليس ذلك جميلا؟ كم هو جميل ذلك التوالي الشكلي، وانظر كم هي رقيقة صغيرة عظمة فخذ الفأر تلك عظمة فخذ رقيقة دقيقة تخص فأرًا رقيقًا دقيقًا. أليس ذلك جميلا؟ لن أتوقف عن الاندهاش من جمال كل تفصيلة من تفاصيل العالم الطبيعي الذي نعيش فيه.
لكن ماذا عن القياسات كيف تتوافق مع معادلاتنا؟ لكن صدمت عندما أجريت الحسابات الرياضية، صُدمت بحق. فقد وجدتُ أن عظمة فخذ الحصان تفوق نظيرتها لدى الفأر طولا بـ 40 مرة، وتنبأت حساباتي بأن سمكها سيفوق سمك عظمة فخذ الفأر بما يزيد عن 250 مرة. لكنها في الواقع كانت تفوقها بـ 70 مرة. لذلك فقد سألتُ نفسي «لماذا لم أطلب منهم عظمة فخذ لفيل؟ فقد كان ذلك سيحسم المسألة». أظنهم انزعجوا مني عندما رجعت إليهم مرة أخرى، لكنهم كانوا من اللطف أن منحوني إياها. لكنني كنتُ وقتها على يقين أنهم منحوني إياها ليتخلصوا مني، وعليكم أن تصدقوني عندما أقول لكم إن حمل هذه العظمة أمر غاية في الصعوبة؛ فطولها يتجاوز ياردة كاملة ووزنها يبلغ طنا. لم أستطع أن أصبر يومها كي أُجري حساباتي الرياضية، ولم أستطع النوم ليلتها مطلقا.
هل تعرف ماذا وجدت؟ وجدتُ أن طول عظمة فخذ الفأر يبلغ 1.1 ± 0.05 سنتيمتر، وسُمكها يبلغ 0.7 ± 0.1 ميلليمتر أي إنها بالغة النحول. بينما يبلغ طول عظمة فخذ الفيل 101 ± 1 سنتيمتر أي نحو مائة مثل طول عظمة فخذ الفأر. أما عن سمك عظمة فخذ الفيل، فوفقًا لقياساتي كانت تبلغ 86 ± 4 ميلليمتر، أي نحو 120 مثل قطر عظمة فخذ الفأر. لكن طبقا لحساباتي، لو كان جاليليو محقا، فمن المفترض أن يفوق سمك عظمة فخذ الفيل نظيرتها لدى الفأر بألف مثل. بعبارة أخرى، كان من المفترض أن يبلغ سمكها 70 سنتيمتر. لكن ما وجدته أنها تبلغ نحو تسع سنتيمترات فقط. ومن ثم فقد خلصت وأنا متردد إلى أن العظيم جاليليو جاليلي كان على خطأ.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
قسم الشؤون الفكرية يقيم الحفل الختامي لمسابقة حفظ قصار السور للناشئة في أفريقيا
|
|
|