


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 7-2-2022
التاريخ: 30-1-2023
التاريخ: 2023-02-04
التاريخ: 2024-05-23
|
We have very fast electrons moving in circular paths in the synchrotron; they are travelling at very nearly the speed c, and it is possible to see the above radiation as actual light! Let us discuss this in more detail.
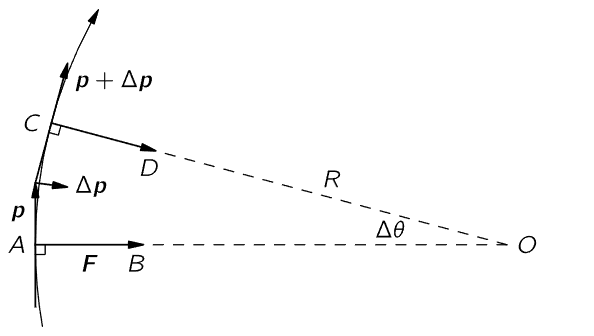
Fig. 34–4. A charged particle moves in a circular (or helical) path in a uniform magnetic field.
In the synchrotron we have electrons which go around in circles in a uniform magnetic field. First, let us see why they go in circles. From Eq. (28.2),
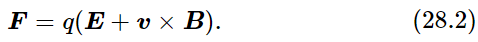
we know that the force on a particle in a magnetic field is given by

and it is at right angles both to the field and to the velocity. As usual, the force is equal to the rate of change of momentum with time. If the field is directed upward out of the paper, the momentum of the particle and the force on it are as shown in Fig. 34–4. Since the force is at right angles to the velocity, the kinetic energy, and therefore the speed, remains constant. All the magnetic field does is to change the direction of motion. In a short time Δt, the momentum vector changes at right angles to itself by an amount Δp=FΔt, and therefore p turns through an angle Δθ= Δp/p= qvBΔt/p, since |F|=qvB. But in this same time the particle has gone a distance Δs=vΔt. Evidently, the two lines AB and CD will intersect at a point O such that OA= OC= R, where Δs=RΔθ. Combining this with the previous expressions, we find RΔθ/Δt= Rω= v= qvBR/p, from which we find
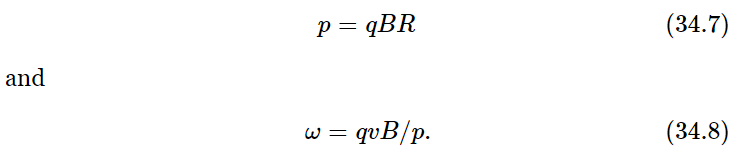
Since this same argument can be applied during the next instant, the next, and so on, we conclude that the particle must be moving in a circle of radius R, with angular velocity ω.
The result that the momentum of the particle is equal to a charge times the radius times the magnetic field is a very important law that is used a great deal. It is important for practical purposes because if we have elementary particles which all have the same charge and we observe them in a magnetic field, we can measure the radii of curvature of their orbits and, knowing the magnetic field, thus determine the momenta of the particles. If we multiply both sides of Eq. (34.7) by c, and express q in terms of the electronic charge, we can measure the momentum in units of the electron volt. In those units our formula is

where B, R, and the speed of light are all expressed in the mks system, the latter being 3×108, numerically.
The mks unit of magnetic field is called a weber per square meter. There is an older unit which is still in common use, called a gauss. One weber/m² is equal to 104 gauss. To give an idea of how big magnetic fields are, the strongest magnetic field that one can usually make in iron is about 1.5×104 gauss; beyond that, the advantage of using iron disappears. Today, electromagnets wound with superconducting wire are able to produce steady fields of over 105 gauss strength—that is, 10 mks units. The field of the earth is a few tenths of a gauss at the equator.
Returning to Eq. (34.9), we could imagine the synchrotron running at a billion electron volts, so pc would be 109 for a billion electron volts. (We shall come back to the energy in just a moment.) Then, if we had a B corresponding to, say, 10,000 gauss, which is a good substantial field, one mks unit, then we see that R would have to be 3.3 meters. The actual radius of the Caltech synchrotron is 3.7 meters, the field is a little bigger, and the energy is 1.5 billion, but it is the same idea. So now we have a feeling for why the synchrotron has the size it has.
We have calculated the momentum, but we know that the total energy, including the rest energy, is given by  and for an electron the rest energy corresponding to mc2 is 0.511×106 eV, so when pc is 109 eV we can neglect mc2, and so for all practical purposes W=pc when the speeds are relativistic. It is practically the same to say the energy of an electron is a billion electron volts as to say the momentum times c is a billion electron volts. If W=109 eV, it is easy to show that the speed differs from the speed of light by but one part in eight million!
and for an electron the rest energy corresponding to mc2 is 0.511×106 eV, so when pc is 109 eV we can neglect mc2, and so for all practical purposes W=pc when the speeds are relativistic. It is practically the same to say the energy of an electron is a billion electron volts as to say the momentum times c is a billion electron volts. If W=109 eV, it is easy to show that the speed differs from the speed of light by but one part in eight million!
We turn now to the radiation emitted by such a particle. A particle moving on a circle of radius 3.3 meters, or 20 meters circumference, goes around once in roughly the time it takes light to go 20 meters. So, the wavelength that should be emitted by such a particle would be 20 meters—in the shortwave radio region. But because of the piling up effect that we have been discussing (Fig. 34–3), and because the distance by which we must extend the radius to reach the speed c is only one part in eight million of the radius, the cusps of the curtate cycloid are enormously sharp compared with the distance between them. The acceleration, which involves a second derivative with respect to time, gets twice the “compression factor” of 8×106 because the time scale is reduced by eight million twice in the neighborhood of the cusp. Thus we might expect the effective wavelength to be much shorter, to the extent of 64 times 1012 smaller than 20 meters, and that corresponds to the x-ray region. (Actually, the cusp itself is not the entire determining factor; one must also include a certain region about the cusp. This changes the factor to the 3/2 power instead of the square, but still leaves us above the optical region.) Thus, even though a slowly moving electron would have radiated 20-meter radiowaves, the relativistic effect cuts down the wavelength so much that we can see it! Clearly, the light should be polarized, with the electric field perpendicular to the uniform magnetic field.

Fig. 34–5. The light which strikes a grating as a single, sharp pulse is scattered in various directions as different colors.
To further appreciate what we would observe, suppose that we were to take such light (to simplify things, because these pulses are so far apart in time, we shall just take one pulse) and direct it onto a diffraction grating, which is a lot of scattering wires. After this pulse comes away from the grating, what do we see? (We should see red light, blue light, and so on, if we see any light at all.) What do we see? The pulse strikes the grating head-on, and all the oscillators in the grating, together, are violently moved up and then back down again, just once. They then produce effects in various directions, as shown in Fig. 34–5. But the point P is closer to one end of the grating than to the other, so at this point the electric field arrives first from wire A, next from B, and so on; finally, the pulse from the last wire arrives. In short, the sum of the reflections from all the successive wires is as shown in Fig. 34–6(a); it is an electric field which is a series of pulses, and it is very like a sine wave whose wavelength is the distance between the pulses, just as it would be for monochromatic light striking the grating! So, we get colored light all right. But, by the same argument, will we not get light from any kind of a “pulse”? No. Suppose that the curve were much smoother; then we would add all the scattered waves together, separated by a small time between them (Fig. 34–6b). Then we see that the field would not shake at all, it would be a very smooth curve, because each pulse does not vary much in the time interval between pulses.
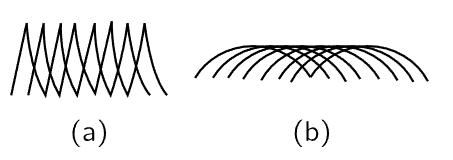
Fig. 34–6. The total electric field due to a series of (a) sharp pulses and (b) smooth pulses.
The electromagnetic radiation emitted by relativistic charged particles circulating in a magnetic field is called synchrotron radiation. It is so named for obvious reasons, but it is not limited specifically to synchrotrons, or even to earthbound laboratories. It is exciting and interesting that it also occurs in nature!



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|