
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Probability wave amplitudes
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 38
2024-04-20
1954
Usually, we have tried to present things accurately, or at least precisely enough that they will not have to be changed when we learn more—it may be extended, but it will not be changed! But when we try to talk about the wave picture or the particle picture, both are approximate, and both will change. Therefore, what we learn in this chapter will not be accurate in a certain sense; it is a kind of half-intuitive argument that will be made more precise later, but certain things will be changed a little bit when we interpret them correctly in quantum mechanics. The reason for doing such a thing, of course, is that we are not going to go directly into quantum mechanics, but we want to have at least some idea of the kinds of effects that we will find. Furthermore, all our experiences are with waves and with particles, and so it is rather handy to use the wave and particle ideas to get some understanding of what happens in given circumstances before we know the complete mathematics of the quantum-mechanical amplitudes. We shall try to illustrate the weakest places as we go along, but most of it is very nearly correct—it is just a matter of interpretation.
First of all, we know that the new way of representing the world in quantum mechanics—the new framework—is to give an amplitude for every event that can occur, and if the event involves the reception of one particle then we can give the amplitude to find that one particle at different places and at different times. The probability of finding the particle is then proportional to the absolute square of the amplitude. In general, the amplitude to find a particle in different places at different times varies with position and time.
In a special case the amplitude varies sinusoidally in space and time like ei(ωt−k⋅r) (do not forget that these amplitudes are complex numbers, not real numbers) and involves a definite frequency ω and wave number k. Then it turns out that this corresponds to a classical limiting situation where we would have believed that we have a particle whose energy E was known and is related to the frequency by
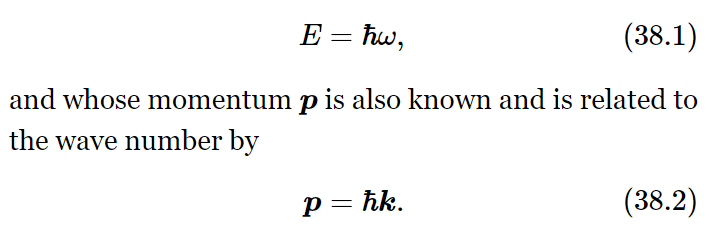
This means that the idea of a particle is limited. The idea of a particle—its location, its momentum, etc.—which we use so much, is in certain ways unsatisfactory. For instance, if an amplitude to find a particle at different places is given by ei(ωt−k⋅r), whose absolute square is a constant, that would mean that the probability of finding a particle is the same at all points. That means we do not know where it is—it can be anywhere—there is a great uncertainty in its location.
On the other hand, if the position of a particle is more or less well known and we can predict it fairly accurately, then the probability of finding it in different places must be confined to a certain region, whose length we call Δx. Outside this region, the probability is zero. Now this probability is the absolute square of an amplitude, and if the absolute square is zero, the amplitude is also zero, so that we have a wave train whose length is Δx (Fig. 38–1), and the wavelength (the distance between nodes of the waves in the train) of that wave train is what corresponds to the particle momentum.
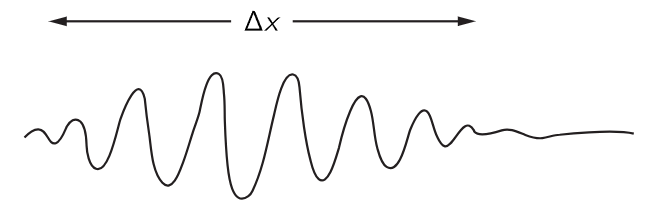
Fig. 38–1. A wave packet of length Δx.
Here we encounter a strange thing about waves; a very simple thing which has nothing to do with quantum mechanics strictly. It is something that anybody who works with waves, even if he knows no quantum mechanics, knows: namely, we cannot define a unique wavelength for a short wave train. Such a wave train does not have a definite wavelength; there is an indefiniteness in the wave number that is related to the finite length of the train, and thus there is an indefiniteness in the momentum.
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















